By pooling resources between cells, colonies of bacteria can exhibit behaviours far beyond the capabilities of an individual bacterium. For example, bacterial populations can encase themselves in a self-generated polymer matrix that shelters cells in the core of the population from the external environment. Such communities are termed “bacterial biofilms”, and show increased tolerance to antimicrobial treatments such as antibiotics. In order to develop medical therapies that circumvent this communal bacterial resistance, it is vital to understand how bacterial cells communicate with one another and work together to display such collective behaviours.
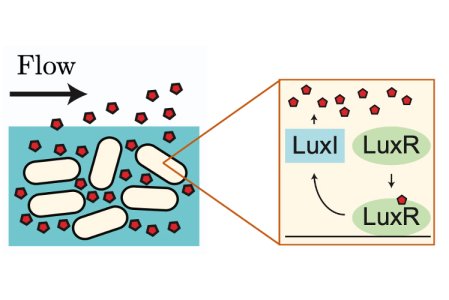
Bacteria use intercellular signalling, or quorum sensing (QS), to share information and respond collectively to aspects of their surroundings. Each bacterium produces QS signalling molecules (autoinducers) that diffuse between cells, providing information about the cellular density of the bacterial colony. However, since autoinducers are exposed to the external environment, they are susceptible to removal by external fluid flow, which is a ubiquitous feature of bacterial habitats ranging from the lungs, gut, and nasal passage to rivers, lakes, and oceans. A key open question is: how are bacteria able to communicate effectively in dynamic flow environments?
Answering this question has been the focus of a collaboration between Oxford Mathematician Mohit Dalwadi and Philip Pearce (Harvard Medical School). In a paper recently published in the Proceedings of the National Academy of Sciences, they developed a mathematical model to understand how bacteria use features of their genetic network to maximise the information gained from QS signalling in the presence of fluid flow (Figure 1).
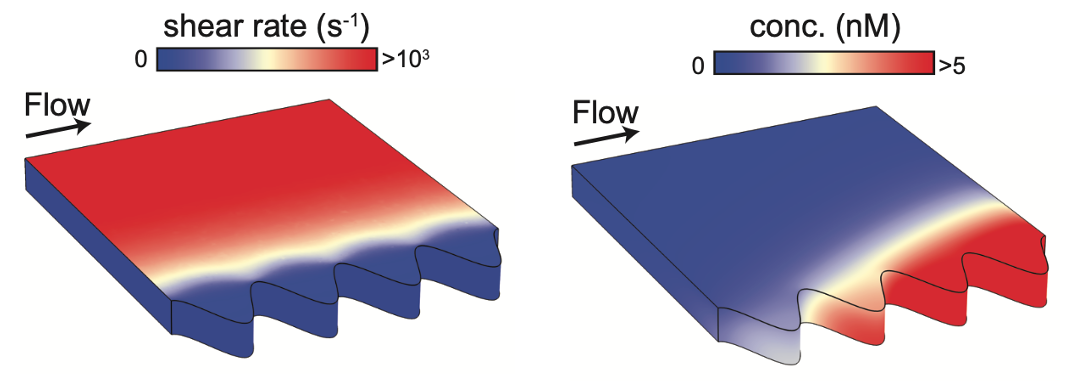
The mathematical model that the duo developed allowed them to explore and quantify how emergent colony behaviours depend on fluid flow. They found that an external flow can suppress QS completely, but that positive genetic feedback between the local autoinducer concentration and its production by each bacterium causes the entire bacterial population to become flooded with signalling molecules if the cell density is above a critical value (Figure 2). By identifying the presence of a bifurcation in the underlying mathematical system, they were able to quantify the critical density in terms of the physical and genetic system parameters, such as the speed of the external flow, the height of the cell layer, and the strength of genetic feedback. Thus, their mathematical analysis yielded a simple and transparent mathematical relationship that linked these various parameters at the critical cell density.
By applying the mathematical relationship that they derived, the duo were able to investigate several different features of bacterial signalling. For example, they explained recent experimental results that showed how QS is promoted in crevices or pores, where bacteria are sheltered from external fluid flow (Figure 3). Furthermore, they showed how a bacterial population can distinguish between changes in cell density and flow rate, by combining different autoinducer signals (Figure 4).
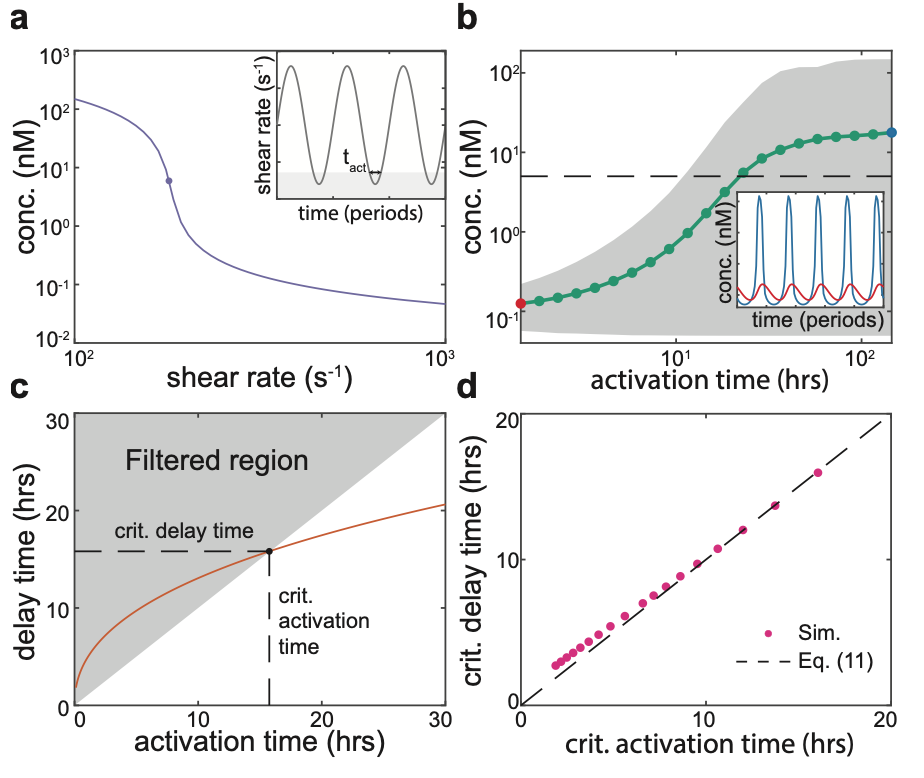
In environments with an oscillatory or noisy flow, such as the lungs or the gut, QS has the potential downside to the bacteria of triggering a premature commitment to multicellular behaviours with a high energy cost (for example, generating extracellular matrix). However, by undertaking a dynamic analysis of the mathematical system, Dalwadi and Pearce found that the properties of the bifurcation at the critical cell density imply that QS signalling carries an inherent robustness to noise (Figure 5) – the stronger the positive genetic feedback in the system, the longer it takes for bacteria to transition to their “activated” state, in which they exhibit multicellular behaviours. This means that, through the genetic properties of their QS signalling system, a bacterial population can sense the average strength of a dynamically oscillating or noisy fluid flow. Overall, by increasing our fundamental understanding of bacterial signalling, this study will help scientists to develop new treatments to bacterial infections that interfere with the formation of bacterial biofilms.
Figure 1: The LuxIR positive feedback system.
Figure 2: At a critical density, a small change in bacterial density can cause the concentration of autoinducers to suddenly increase. This is the onset of QS activation.
Figure 3: In complex geometries, positive feedback causes robust QS activation which is initiated in deeper crevices and downstream.
Figure 4: Bacteria can distinguish between changes in density and flow by measuring the activation of just two different autoinducers, splitting parameter space into four regions A, B, C, and D.
Figure 5: There is an inherent delay associated with dynamically crossing the bifurcation that marks the onset of QS activation. This filters out incursions into the activated region that are shorter than the inherent delay time.