Oxford Mathematician Ben Green on a tale of conjectures, mistaken assumptions and eventual solutions: a tale of mathematics.
"The famous discrete mathematician Ron Graham sadly passed away last year. I did not know him well, but I had the pleasure of meeting him a few times. On the first such occasion, in Vancouver in 2004, he mentioned one of his favourite open questions over lunch. This concerns the size of certain "van der Waerden numbers", a kind of arithmetic variant of graph Ramsey numbers.
Fix a positive integer $k \geq 3$, and let $N(k)$ be the smallest value of $N$ such that the following is true: however you colour the integers $\{1,\dots,N\}$ red and blue, there is always either (i) a blue arithmetic progression of length 3 or (ii) a red arithmetic progression of length $k$ (or both). That there exists such a value of $N(k)$ is not a trivial fact, but it is a consequence of a celebrated theorem of van der Waerden from the 1920s. In fact, it is now known that $N(k)$ grows at most exponentially as a function of $k$.
What about the true value? There is cast-iron numerical data up to about $k = 20$, and conjectured values up to about $k = 40$, obtained with computer searches. The numerics very strongly suggest that $N(k)$ is roughly $k^2$. For instance, it is believed that $N(20) = 389$ and $N(30) = 903$. The question Ron Graham asked me in 2004 was this: is it true that $N(k) < Ck^2$ for some absolute constant $C$, and for all $k$? When Ron asked me this question I immediately told him that I thought the answer was no, and I thought I would send him a proof within a few days. My reasoning was as follows. There are well-known examples of (for instance) subsets of $\{1,\dots, k^{10}\}$ of size $k^{9.9}$ with no three-term arithmetic progressions, provided $k$ is sufficiently large. Take a set like this, and colour it blue. Colour the remaining points red. There are quite a lot of red points but, unless something unexpected happens, one would still not anticipate red arithmetic progressions of length much longer than about $k^{0.1}$, and certainly nowhere near as long as $k$. (One can actually make this rigorous: if the blue points were a random subset of size $k^{9.9}$, then almost surely (as $k \rightarrow \infty$) what I just wrote is true.)
Unfortunately, something unexpected does happen. For all the well-known examples of large sets free of three-term progressions, their complements contain extremely long arithmetic progressions. In particular, none of these examples provide a disproof of Ron Graham's conjecture. I apologized to Ron for not believing his conjecture, and to make amends I repeated it myself in print.
However, in recent work I have shown that the conjecture is, after all, false. Not only is $N(k)$ not bounded by a quadratic, but in fact it is not bounded by any polynomial. It grows at least as quickly as roughly $e^{(\log k)^{4/3}}$.
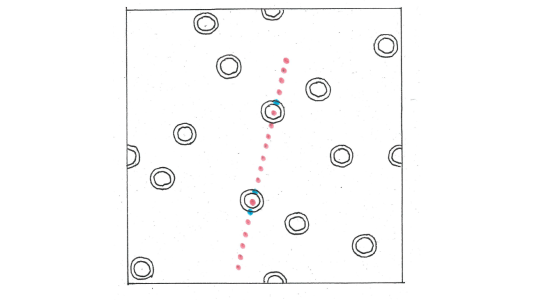
The red-blue colouring which shows this is rather elaborate. Very roughly, one sets up a discrete-time dynamical system on a high-dimensional torus given by an irrational rotation. On the torus one takes a large, randomly-chosen, collection of very thin ellipsoidal annuli, all with the same eccentricity, but with this eccentricity also chosen randomly. Then, we colour $n$ blue if $n$ is a return time of our dynamical system to this set of annuli. All other $n$ are coloured red.
By far the hardest part of the proof is to show that (with high probability) this colouring does not contain long red progressions. This occupies about 50 pages and uses tools from harmonic analysis, the geometry of numbers, combinatorics and random matrix theory.
Despite this new result, the gap between the known upper and lower bounds for $N(k)$ remains close to exponential and seems likely to remain so for the foreseeable future."