Deep learning has become an important topic across many domains of science due to its recent success in image recognition, speech recognition, and drug discovery. Deep learning techniques are based on neural networks, which contain a certain number of layers to perform several mathematical transformations on the input. A nonlinear transformation of the input determines the output of each layer in the neural network: $x \mapsto \sigma(W x + b)$, where $W$ is a matrix called the weight matrix, $b$ is a bias vector, and $\sigma$ is a nonlinear function called the activation function.
Each of these variables contain several parameters, which are updated during the training procedure of the neural network to fit some data. In standard image classification problems, the input of the network consists of images, while the outputs are the associated labels. The computational cost of training a neural network depends on its total number of parameters. A key question in designing deep learning architectures is the choice of the activation function.
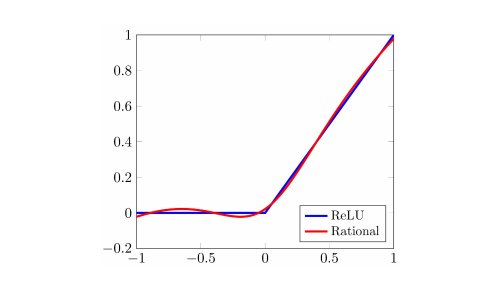
Figure 1. A rational activation function (red) initialized close to the ReLU function (blue).
In a recent work, Oxford Mathematicians Nicolas Boullé and Yuji Nakatsukasa, together with Alex Townsend from Cornell University, introduced a novel type of neural networks, based on rational functions, called rational neural networks [1]. Rational neural networks consist of neural networks with rational activation functions of the form $\sigma(x)=P(x)/Q(x)$, where $P$ and $Q$ are two polynomials. One particularity is that the coefficients of the rational functions are initialized close to the standard ReLU activation function (see fig 1) and are also trainable parameters. These type of networks have been proven to have higher approximation power than state-of-the-art neural network architectures, which means that they can tackle a variety of deep learning problems with fewer number of trainable parameters.
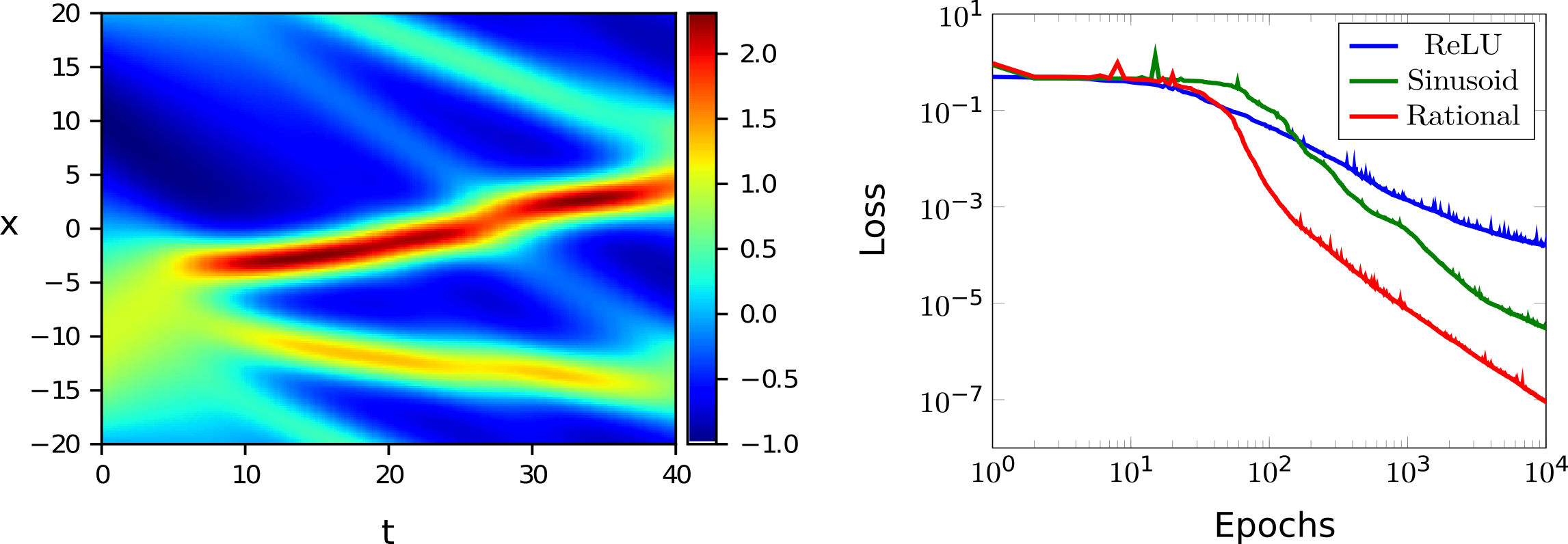
Figure 2. Two-dimensional function learned by a rational neural network (left) and loss function during training compared with standard architecture (right).
Rational neural networks are particularly suited for regression problems due to the smoothness and approximation power of rational functions (see fig 2). Moreover, they are easy to implement in existing deep learning architectures such as TensorFlow or PyTorch [2]. Finally, while neural networks have applications in diverse fields such as facial recognition, credit-card fraud, speech recognition, and medical diagnosis, there is a growing need for understanding their approximation power and other theoretical properties. Neural networks, in particular rational neural networks, have the potential to revolutionize fields where mathematical models derived by mechanistic principles are lacking [3].
1. Boullé, Nakatsukasa, Townsend, Rational neural networks, NeurIPS 33, 2020.
2. GitHub repository, 2020.
3. Boullé, Earls, Townsend, Data-driven discovery of physical laws with human-understandable deep learning, arxiv:2105.00266, 2021.