Arun Soor - Origami Spiral

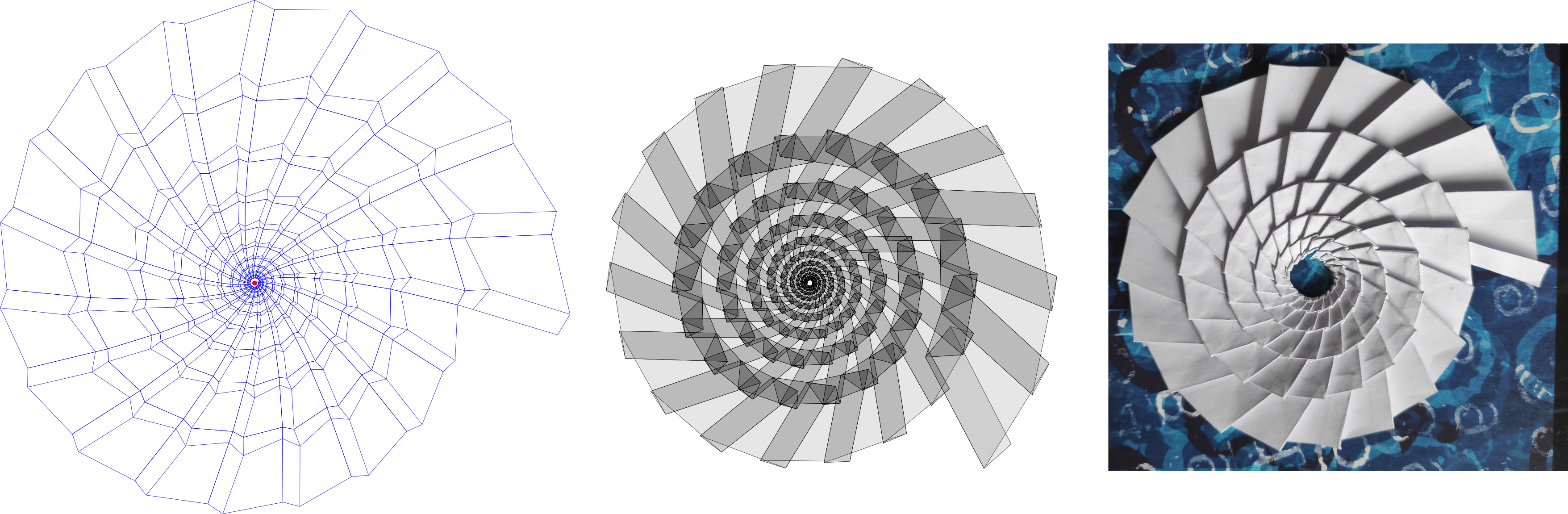
It is an origami spiral designed using group theory. The idea is to design a unit cell that is compatible with a “spiral group” of fixed chirality, in both the folded and unfolded states. These spiral groups are generated by a pair of commuting affine linear transformations whose powers “spiral in” towards a fixed point. We use “discrete” groups so that the spiral will meet up with itself again.

The orbit of the unfolded unit cell under one discrete group tells us which creases we must fold along; then we arrange so that the folded state is the orbit under another discrete group (and therefore compatible). 

In practice, this means solving some constraints on the unit cell. The discreteness condition adds a constraint to the angles and the ratios of side lengths. Additionally, to ensure that the structure will fold flat, we need that the alternating sum of angles between creases around each vertex is 0 – this is known as Kawasaki’s condition.

Arun Soor is an undergraduate student at St John's College.