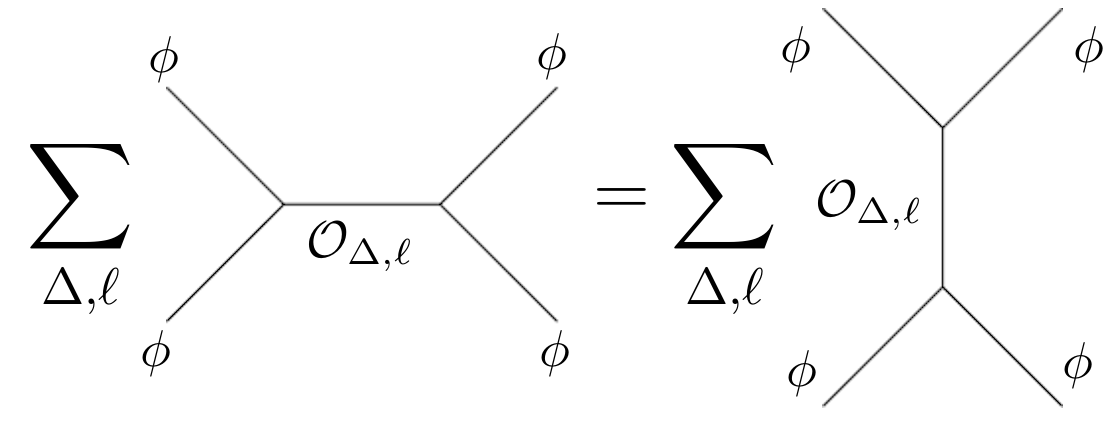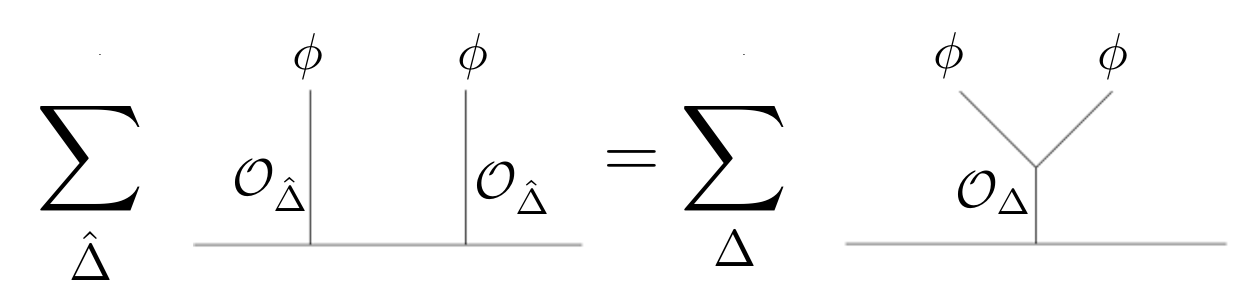Oxford Mathematician Connor Behan discusses the ways in which a free quantum field can be coupled to a spatial boundary. His recent work with Lorenzo di Pietro, Edoardo Lauria and Balt van Rees sheds light on this question using the non-perturbative bootstrap technique.
"In a material undergoing a second order phase transition, the critical behaviour is described by one of the scale invariant field theories. In the space of quantum field theories (which form the backbone of theoretical physics), these are distinguished points which are under better mathematical control. More precisely, exciting progress has been made in the study of conformal field theories (CFTs) where by conformal transformation, we mean any map which preserves angle. A simple example is a holomorphic function, and indeed, early work on CFTs focused on two dimensions where it is possible to exploit this deep connection.
Much of my research concerns the fact that CFTs in all dimensions posess an operator algebra - a product of two fields $\phi(x_1) \phi(x_2)$ can be written as a convergent sum of local operators $\mathcal{O}(x)$ at a third point. This allows CFTs to be characterized by a discrete set of numbers called the spins and scaling dimensions $(\ell_i, \Delta_i)$ which we are interested in constraining. To demonstrate a key technique, a correlation function with four copies of $\phi$ can be computed in different ways depending on which pairs are "fused'' together. This leads to the equation \begin{equation} \sum_{\Delta, \ell} c^2_{\Delta, \ell} G_{\Delta, \ell}(x_1, x_2, x_3, x_4) = \sum_{\Delta, \ell} c^2_{\Delta, \ell} G_{\Delta, \ell}(x_3, x_2, x_1, x_4), \quad\quad (1) \end{equation} where $G_{\Delta, \ell}$ is a known special function. Crucially, the coefficients are non-negative which means we can be ignorant of their precise values and still investigate the conditions for (1) to have a solution. With the help of convex optimization, this leads to rigorous bounds on $(\ell_i, \Delta_i)$ which must be obeyed by all valid theories.
This story becomes richer when we consider theories on a half space, thus allowing us to talk about a $d$ dimensional bulk and a $d - 1$ dimensional boundary. Boundary correlators obey the same CFT axioms as before but the bulk has new ingredients because some of the conformal symmetry there is broken. As a result, one can already see non-trivial correlation functions with two points. From these, a consistency condition of the form \begin{equation} \sum_{\hat{\Delta}} b^2_{\hat{\Delta}} F^\partial_{\hat{\Delta}}(x_1, x_2) = \sum_{\Delta} a_{\Delta} c_{\Delta} F^B_{\Delta}(x_1, x_2) \quad\quad (2) \end{equation} may be extracted. However, it only has manifestly non-negative coefficients on the left hand side. There have been many attempts to sidestep this problem but most of them require model dependent input or a small parameter in which to expand. Alternatively, if one restricted her attention to the boundary in order to continue working with four-point functions, the bounds obtained would be very weak. In particular, they would need to allow for strange phenomena in which energy seemingly disappears in one place and reappears in another. This process is only revealed to be a local one, where energy moves through the bulk, in the unrestricted system governed by (2).
In work that appeared in 2020, my collaborators and I developed a hybrid approach which combines both points of view. The first step is to pick a conformal field theory which is well understood on the whole space in $d$ dimensions. As a proof of concept, we picked the free massless scalar since it obeys the wave equation \begin{equation} (\Box_x + \partial_y^2) \phi = 0. \label{eom} \end{equation} The second step is to introduce a half space with respect to the $y$ variable, leading to \begin{equation} \phi(x, y) = b_1 \left [ \phi(x, 0) + \dots \right ] + \frac{b_2}{y} \left [ \partial_y \phi(x, 0) + \dots \right ]. \label{sol} \end{equation} We can then use model dependent analogues of (2) to search for exact relations. One of them says that $b_1$ and $b_2$ are fixed in terms of a single parameter in the interval $[-2^{2 - d}, +2^{2 - d}]$ which we call $a_{\phi^2}$. Another one says that at $y = 0$, the three-point functions $\left < \phi \phi \mathcal{O} \right >$, $\left < \phi \partial_y \phi \mathcal{O} \right >$ and $\left < \partial_y \phi \partial_y \phi \mathcal{O} \right >$ are all related to one another by a conformally covariant integral operator. This last statement is especially interesting since it can be phrased entirely in terms of boundary modes. Moreover, after some algebra, it can be put on the same footing as other constraints commonly used in convex optimization problems. This makes it safe to zoom in on the boundary for the last step.
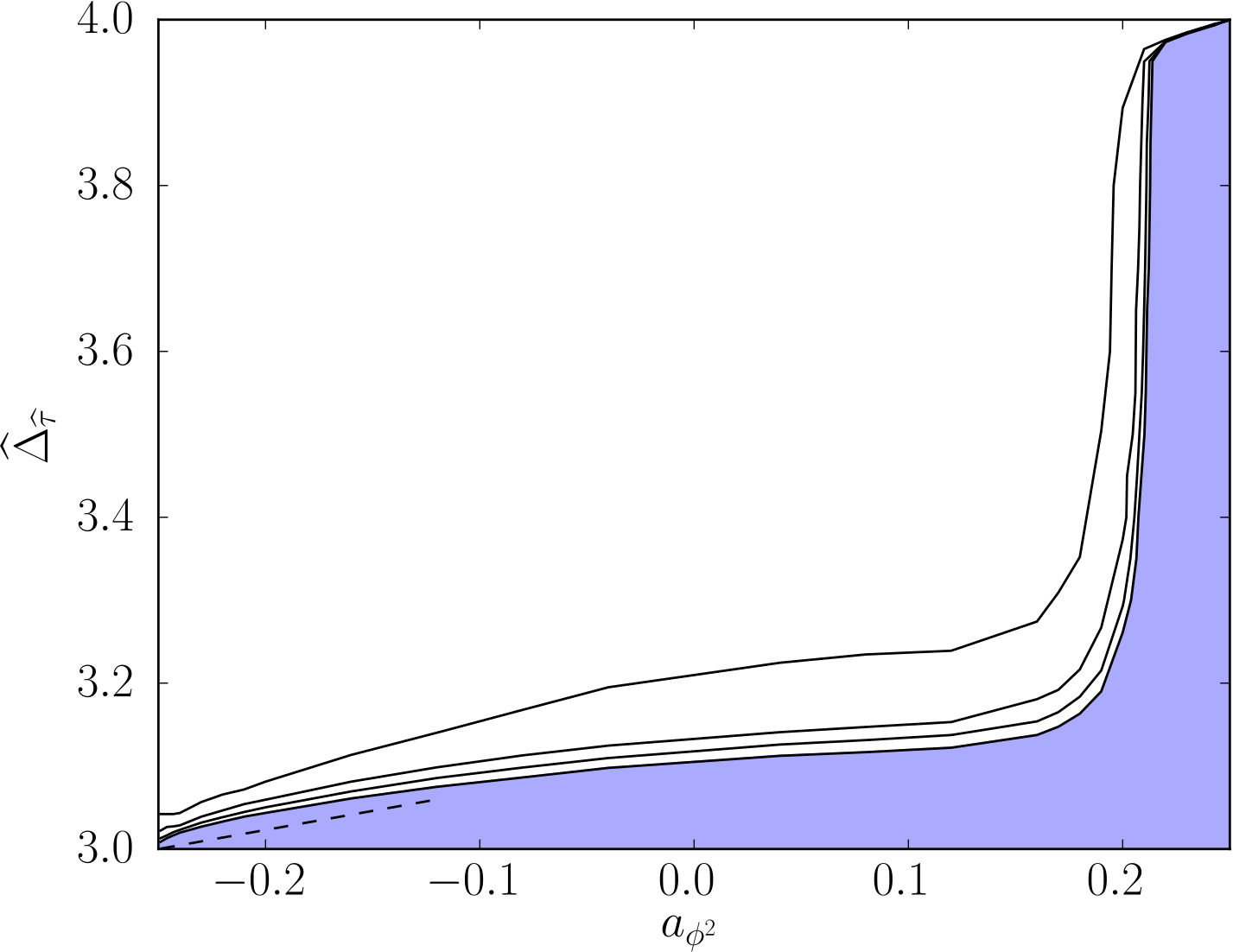
Figure 1: allowed values for the dimension of a spin-2 boundary operator as a function of the bulk one-point function of $\phi^2$. Sub-optimal curves show how the bound converges as numerics are improved.
Our final results are produced by applying (1) to four-point functions on the whole space in $d - 1$ dimensions. This analysis benefits greatly from the exact relations which encode the effect of the bulk. One result which surprised us is an upper bound on the scaling dimension of the simplest spinning operator $\hat{\tau}^{\mu\nu}$ in $d = 4$. The value of 3 on the left hand side can be understood by thinking about the two simplest boundary conditions for the wave equation - the ones realized on either end of a wind instrument. These are Dirichlet and Neumann, which have $b_1 = 0$ and $b_2 = 0$ respectively. Conversely, other points on the curve (provided they are physical) must correspond to more exotic theories which have boundary localized interactions. In other words, the free massless scalar is coupled to additional degrees of freedom which live only on the boundary. Our work is about bootstrapping these boundary localized interactions because it is part of a long tradition of studying CFTs using nothing but the principles of CFT itself. In the past, it has proven fruitful to regard "kinks'' in the bounds as places where a physical theory is likely to sit. This is exactly what appears on the right hand side of the plot, where the dimension of $\hat{\tau}^{\mu\nu}$ jumps almost to 4. We are still having fun thinking about what this newly bootstrapped theory might be."