Oxford Mathematician Aymeric Vie, first year DPhil student at the Centre for Doctoral Training, Mathematics of Random Systems, describes his work on the population network structure of genetic algorithms.This work identifies new ways to improve the performance of those stochastic algorithms, and has received a Best Paper Award at the Genetic and Evolutionary Computation Conference 2021.
A Genetic Algorithm (GA) is a population-based search algorithm invented in the 70s by John Holland. Inspired by Darwin's theory of evolution, the GA simulates some of the evolution processes: selection, fitness, reproduction, crossover, mutation. Facing a given problem described by an objective function, the algorithm samples at random a population of initial solutions in a given search space. Individual solutions' fitness is measured so that most promising solutions are recombined together, while all can encounter mutations, i.e. applications of noise. These steps are iterated for a large number of generations. Being gradient free and capable of exploring very large or deceptive fitness landscapes, those methods have been quite popular in many domains.
When two solutions are recombined together, they have previously been selected for their fitness, i.e. their ability to solve a given problem instance. This is usually measured using a fitness function, other words for an objective or a reward function. In the standard GA thus, any pair of solutions can be recombined together to give birth to new, potentially better solutions. In network science terms, this is equivalent to assuming that there exists a complete network in the population of solutions, in which everyone is connected to everyone.
However, in nature as in social systems, such complete networks are actually quite rare. Individuals in these contexts usually interact with a tiny subset of the whole population, and these interactions are often not random, but characterised by locations, or similarity: we are more likely to interact with people that are geographically, or on other characteristics, similar to us.
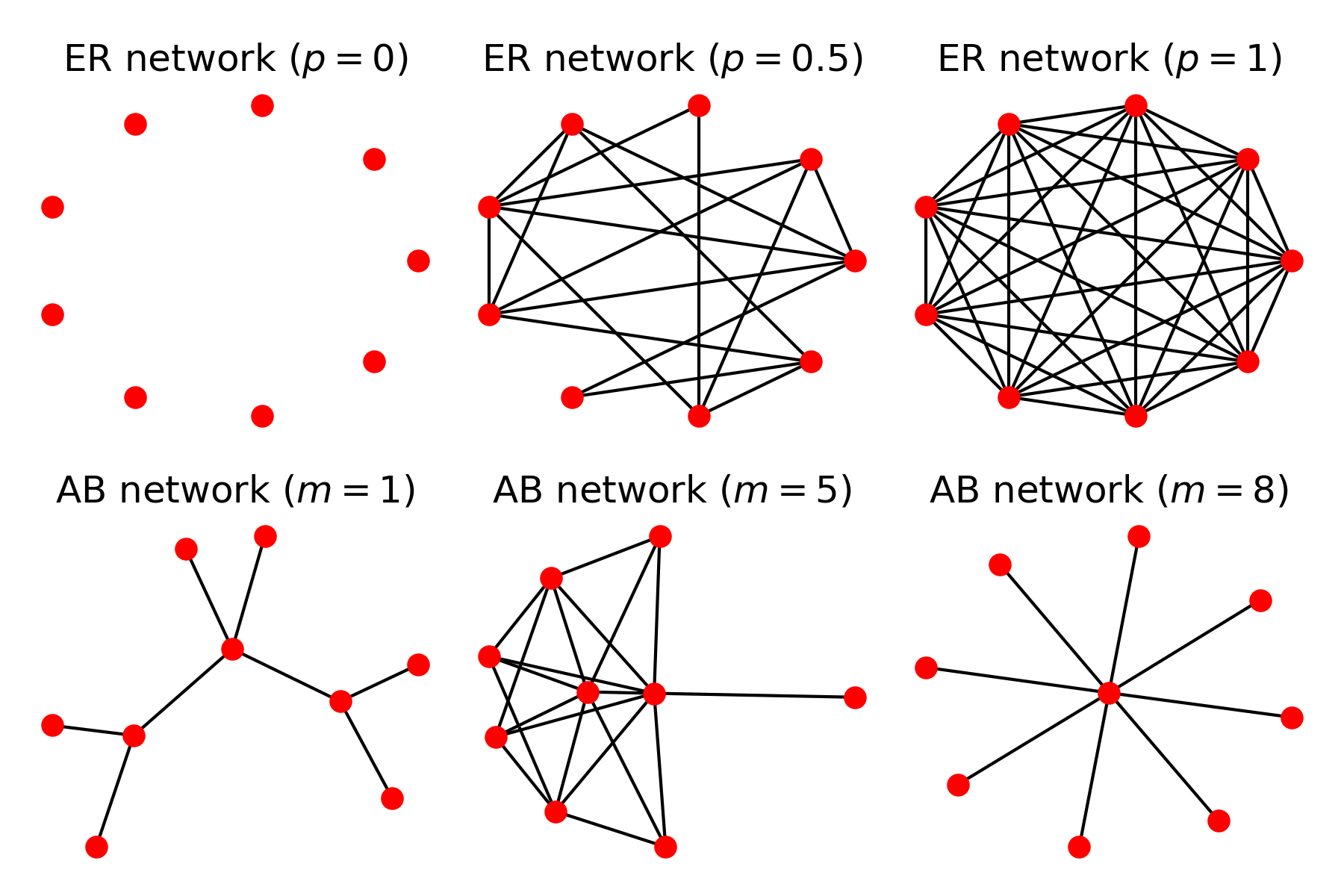
The standard GA, and in fact, most other evolutionary algorithms, carry this implicit assumption of the complete population network. I wondered what would happen to the performance of the GA as an optimisation tool if we were performing this evolution of optimal solutions under alternative network structures. The article explored two main network types: Erdos-Renyi and Albert-Barabasi networks, that both give rise to the high variety of structures shown in Figure 1.
Figure 1: Varied structures obtained from Erdos Renyi (ER) and Albert-Barabasi (AB) networks. ER networks are described by a probability $p$ of existence of a link between a pair of nodes, showing the empty (top left) and complete (top right) networks. AB networks simulate network growth with preferential attachment (mechanism of the type highly cited papers are more likely to be cited by new incoming papers) strength $m$, giving tree networks (bottom left) or even star networks (bottom right).
The resulting Networked Genetic Algorithm (NGA) constrains recombination between individuals as a function of a network structure drawn once at the beginning of search. To identify the impact of network structure on GA performance, I used the networked GA with various network structures to solve instances of minimisation problems. The optimisation performance of the algorithms was evaluated measuring how close and how fast the solutions evolved by the program matched the known global optimum for the optimisation tasks.
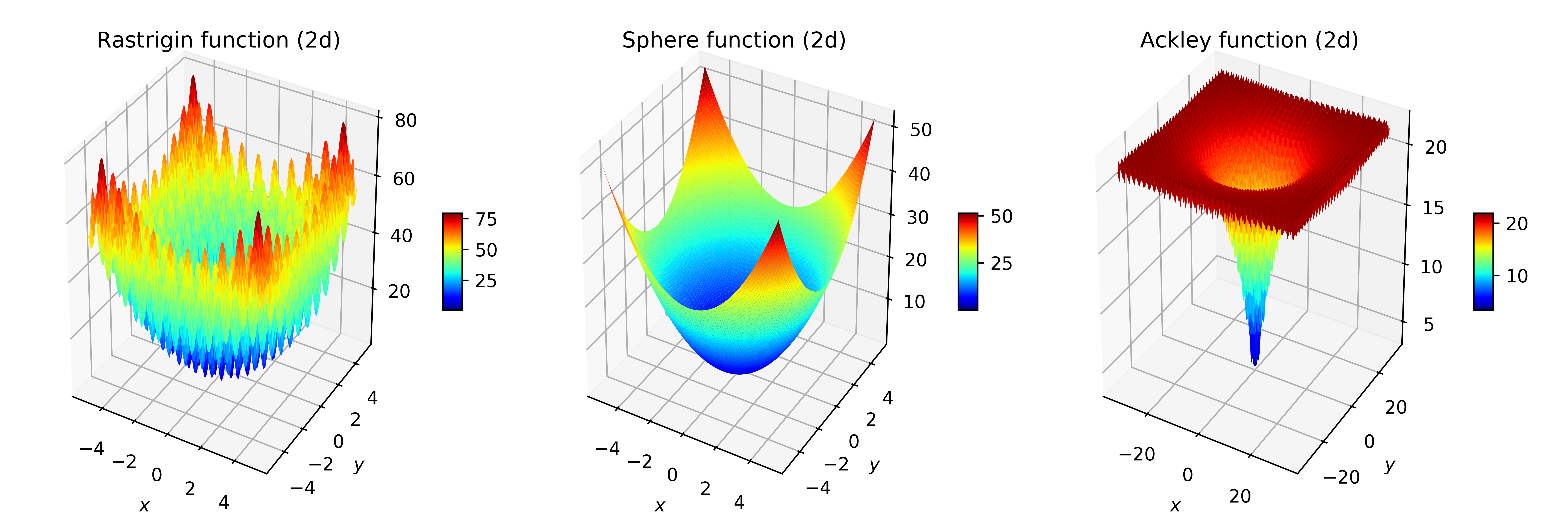
Three standard functions in optimisation were used: the Sphere function, a very smooth, convex, easy to optimise function; and the Rastrigin and Ackley functions, that display many local optima, and very rugged structures that make them difficult for randomised search heuristics. Figure 2 plots the fitness landscape of those functions.
Figure 2: Fitness landscapes of the Rastrigin, Sphere and Ackley functions in two dimensions, for commonly used intervals for the arguments.
The results were richer than expected. They showed a clear impact of network structure over optimisation performance. Networks that were disconnected, i.e., that had sets of nodes not connected to other sets, were struggling to maximise the functions. Networks that were not dense enough, or too centralised, failed similarly. The best results were obtained for networks with intermediate levels of density and low average shortest path length, i.e., an average low number of nodes to cross to go from any node to any other. Those seemingly optimal networks resemble the modular networks frequent in biology.
An unexpected and much welcome finding was that the standard complete GA was actually not the optimal structure. For all the structures of ER and AB networks, the best NGA structure displayed a performance superior by more than 50% to the standard complete network GA.
Assessing further the robustness and generalisability of those findings could place population network structure optimisation as one tool to significantly improve the performance of evolutionary algorithms. The implications of this could be wide reaching, as such complete network structure is implicit in most randomised search heuristics used in Evolutionary Computation. This work also opens the possibility of self-adaptive network structures in evolutionary algorithms, a new paradigm in which the network structure of the algorithm could be continuously optimised during search to further improve performance.