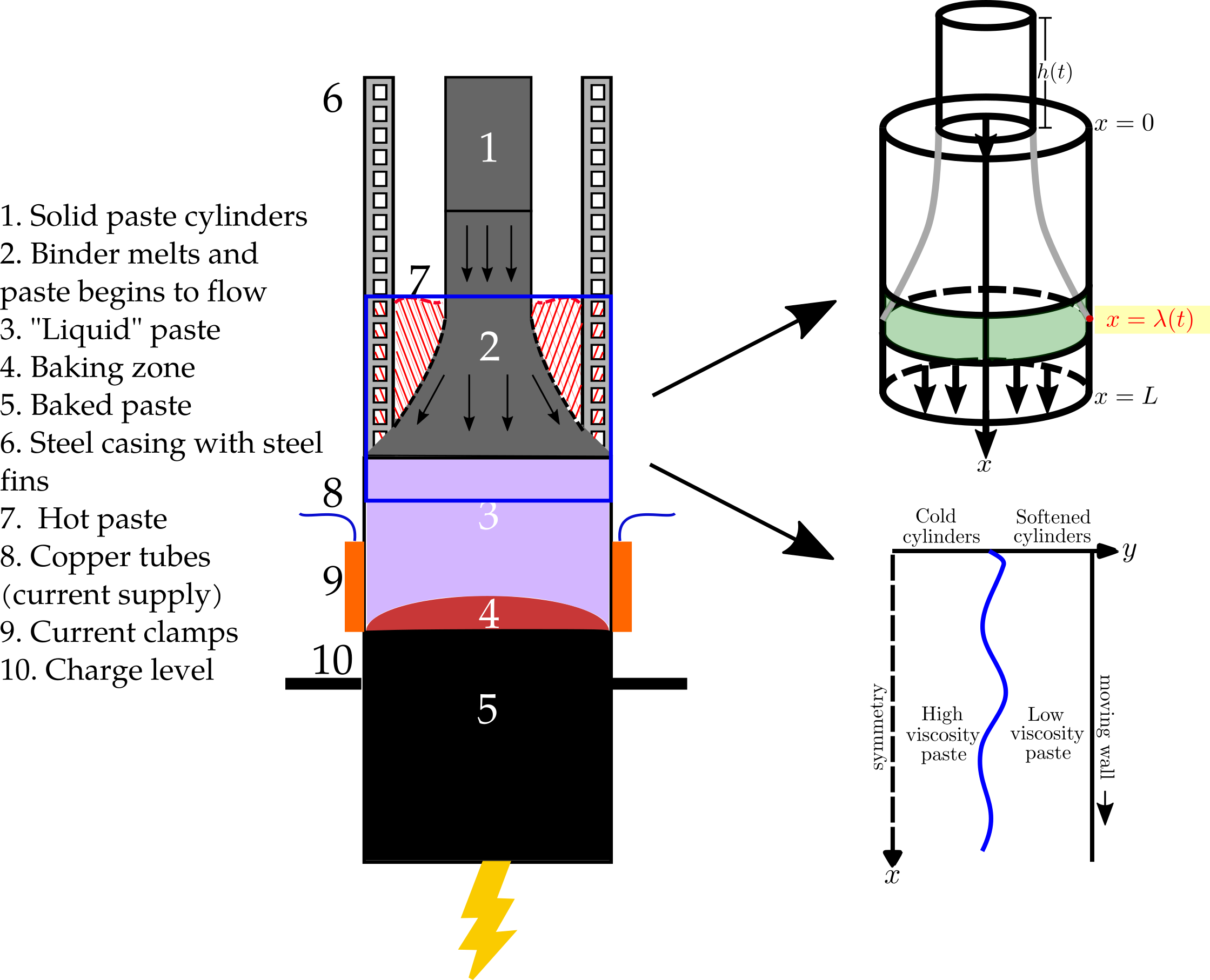
The 7m length by 2m diameter cylindrical Søderberg electrode is the secret behind a yearly production capacity of 215,000 tonnes of silicon for Elkem ASA, the third largest silicon producer in the world. This electrode operates continuously thanks to its raw material: carbon paste, whose viscosity depends very sensitively on the temperature. The paste softens, flows, and then bakes at about 350°C; the baked portion of the paste generates the strong electric arcs that heat up the furnace to 2000°C and power the entire production process. Heat is supplied by fans blowing hot air along the walls, and induced in the steel tube by the current supplied by the copper tubes. A schematic of the electrode and its components is shown in Figure 1 below.
Throughout the years, demand has required electrode sizes and equipment to be changed, which has led to an imbalance in the melting process, making the cylinders sink down into the liquid paste, which results in an electrode with non-uniform material properties. In particular, unwanted electrical induction near the copper tubes that supply the current (item 6 in Figure 1) can lead to such issues, resulting in breakages, fires, and explosions. Among other things, Elkem ASA are interested in understanding how to avoid situations which may lead to such problems. This has led to a productive industrial collaboration between Aasgeir Valderhaug and Ben Sloman at Elkem ASA, and Oxford Mathematicians Ian Hewitt, Peter Howell, and myself, Alissa Kamilova, with the aim of understanding the softening process of the paste and, for example, how changes in cylinder addition may affect it.
Figure 1
Using asymptotic techniques, we have derived the extensional flow time dependent mathematical model coupled with temperature represented in the top right schematic in Figure 1 to describe the paste softening process. Our modelling efforts were initially inspired by previous collaborations between Elkem ASA and Oxford Mathematician Andrew Fowler. We consider the effects of hot air heating, applied on the casing as a function of x, and the unwanted electrical induction, a source term represented by the green shaded region. The location where the paste touches the casing for the first time, λ(t), is a free boundary so it is an output of the model and in particular, when the paste does not reach the casing in this domain, we interpret it as a catastrophic failure of the process. Cylinder addition effects are incorporated into the boundary condition on x=0 at the top of the domain. In practice, 1 to 3 cylinders are added daily, although at times up to two days are skipped. Our mathematical model can replicate examples of these addition schedules and examine the differences in the paste softening process.
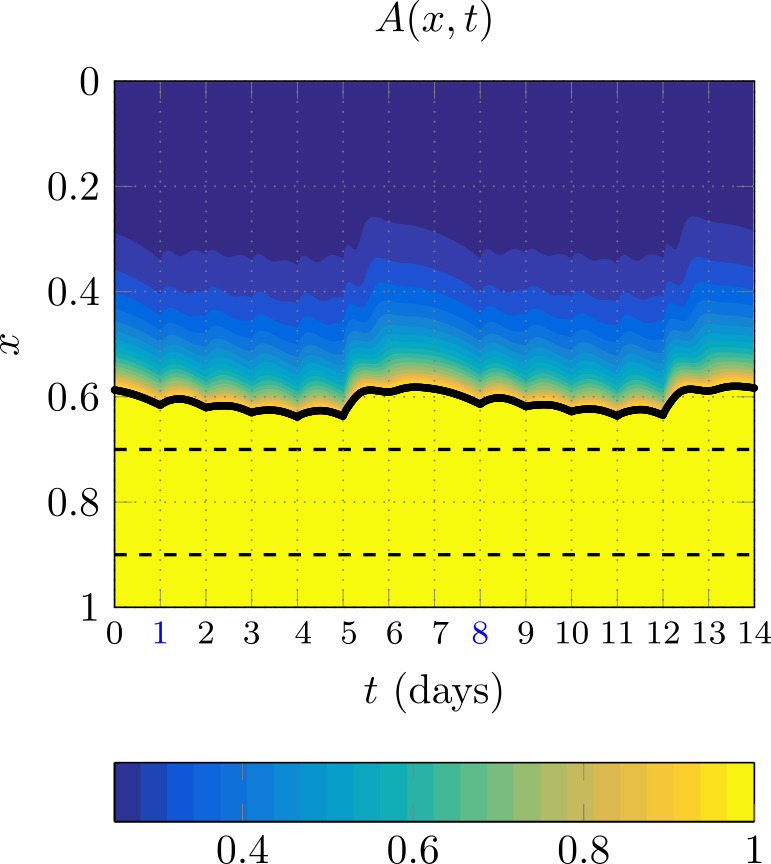
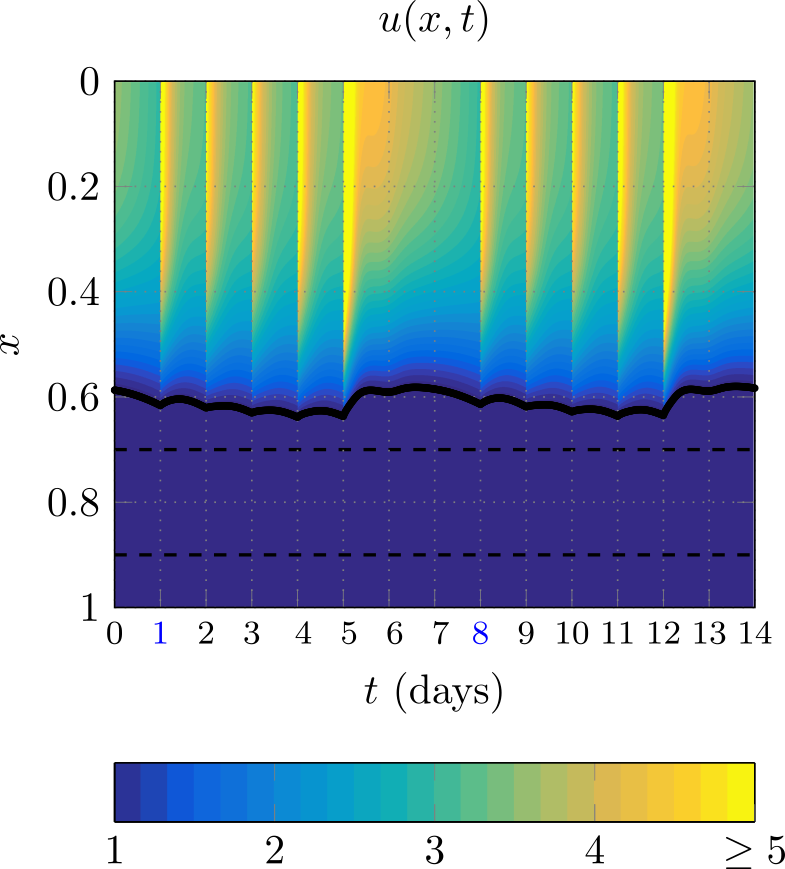
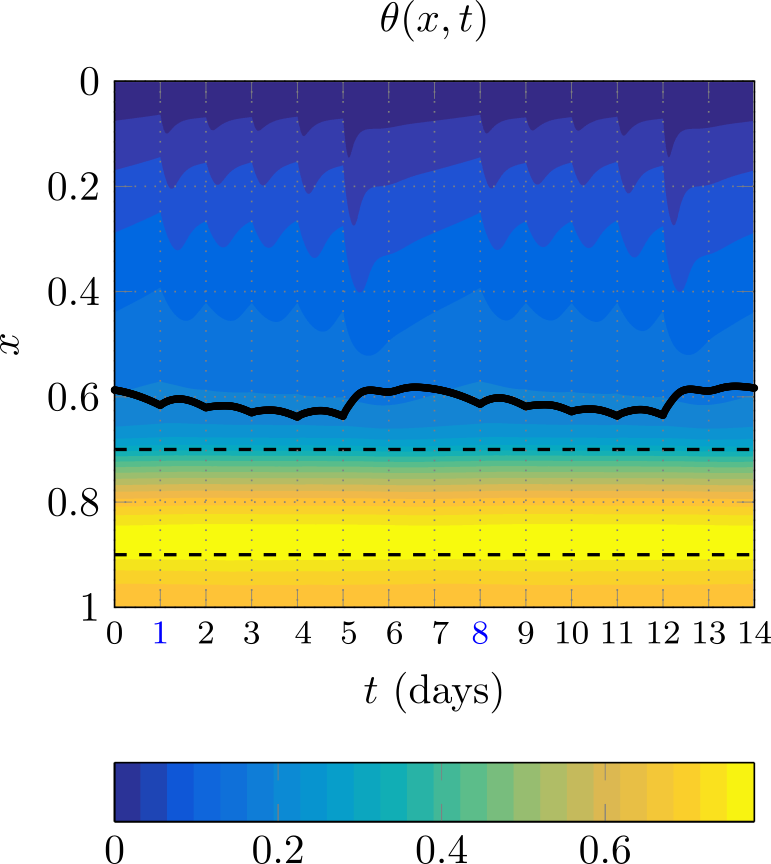
In Figure 2 we show how the area A, velocity u, and temperature θ change as paste is softened, where the black line shows the evolution of the free boundary λ. The time-dependence of the pressure exerted by the added cylinders has the most immediate and dramatic effect on the velocity u. In contrast, the profiles of A and θ indicate that the paste only begins to soften and deform significantly around x=0.3. There are relatively small but noticeable fluctuations in A and θ within each day and not only at the addition times. Furthermore, we found that the large additions every 5th day cause cold paste to be pushed downwards with a large velocity, which causes λ to decrease (move upwards), producing the initial change in this free boundary. Because this paste is colder, however, it does not spread as easily, which causes λ to increase again temporarily, leading to the local minimum observed in the black line in Figure 2. Such behaviours could be observed in reality when cylinder addition days are skipped and our simplified model is a first step in understanding them.
In addition to this work, we have exploited the small aspect ratio ϵ of the electrode as well as the strong temperature-dependent viscosity to derive the simplified steady model depicted in the bottom right schematic in Figure 1. We found that a new distinguished limit emerges when the viscosity variation across the domain is of order 1/ϵ2, resulting in a new hybrid model that contain elements of both lubrication theory and extensional flow. The model describes an approximate plug flow of the cold cylinders down the centre of the domain while hotter low-viscosity paste flows along the sides, and shows good agreement with costly CFD computations of a more complex version of this problem.
Collaborations between industrial partners and mathematicians are not only beneficial for the specific application relevant to the company but also allow us to look at interesting mathematical problems from a fresh perspective, leading to research and innovation that is beneficial for both parties.
Figure 2