If you have ever watched the movie Transformers you may not have worried too much about whether it is realistic. Nevertheless, scientists have tried, and are still trying, to create objects that can transform their shape. The ability to change shape is as important to an emerging class of engineering applications as it is to biological organisms: just as animals and plants morph in response to external stimuli, robots must be able to change shape to adapt to different environments and complete different tasks. Structures that transform shape from one shape to another are called shape-morphing structures.
One of the simplest objectives for a shape-morphing structure might seem to be to transform a flat two-dimensional (2D) sheet into a three-dimensional (3D) structure. However, this apparently simple task involves confronting a series of geometrical and mechanical challenges. The primary challenge arises from a combination of geometry and mechanics: many morphing structures are thin and, as a result, prefer to bend in response to applied loads, rather than to change their length/area. However, Gauss’ Theorema Egregium (the remarkable theorem) states that deformations that preserve length or area (isometries) cannot change the Gaussian curvature of a surface. As a result of the ‘remarkable theorem’, thin sheets cannot ordinarily transform to a doubly-curved object: just think about wrapping an orange with a piece of tissue paper: extra area has to be wasted in folds (see picture above). The geometric incompatibility of a sheet and a sphere is further illustrated by map-makers: all maps must use a distortion of areas to allow a projection of the earth’s curved surface onto a flat piece of paper. For shape-morphing structures, this geometric incompatibility makes it difficult to achieve a particular 3D target structure with non-zero Gaussian curvature from a 2D flat sheet.
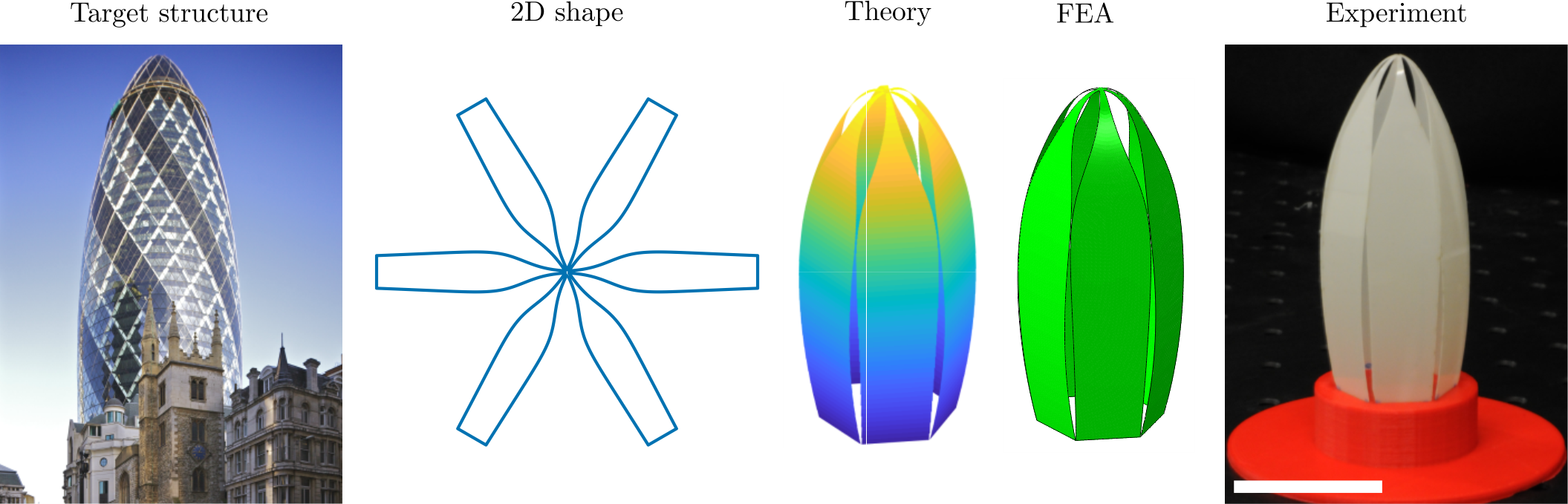
A way forward, or rather around, is suggested by the design strategies for flexible electronic devices: making oriented cuts/slits in a material allows the surface to buffer changes in length/area allowing the possibility of generating 3D shapes that appear to have Gaussian curvature different to the flat sheet as in the picture above (this is only an appearance of a change in Gaussian curvature – locally the sheet preserves its Gaussian curvature). The challenge then becomes how to choose the cut patterns in a 2D sheet to form particular 3D shapes in this way. In a recent study [1], Oxford Mathematicians Mingchao Liu, Lucie Domino and Dominic Vella propose a general inverse design framework for forming apparently axisymmetric 3D structures by harnessing the buckling of multiple tapered elastic sheets (the legs) connected in a central portion (the body). Together this creates a 2D spider-like structure that morphs in 3D: a spider-morph.
Different from most of the previous design methods, which largely proceed by trial and error, the approach proposed in this work relies on using the formalism of the ‘tapered elastica’ equation to describe the deformation of each leg of the spider under both horizontal and vertical loads applied at its edges, outlining a general strategy for the inverse design of shape-morphing structures. By choosing representative architectural structures as targets, the team demonstrate the design paradigm – design spider-morphs – by tapering the widths of the legs such that they deform into axisymmetric 3D structures with positive (30 St Mary Axe, “The Gherkin”), negative (the Eiffel Tower), and variable (the cupola of St. Thomas Church, Lymington) apparent Gaussian curvature. They conduct both numerical simulations and physical experiments to verify the theoretical approach.
One obvious feature of the shapes formed in this way is that it leaves large gaps between the deformed legs. Allowing the thickness of the sheet to change as well as the tapering, gives an extra degree of freedom that allows the 3D shape to be designed and the edges to close. This can be used to make a spider-morph design that when loaded closes to form a globe. While this will not revolutionize map-making, it is inspiring designers to think again about what shapes can be created from simple elements like beams and struts [2].
References:
[1] Liu, M., Domino, L., & Vella, D. (2020). Tapered elasticæ as a route for axisymmetric morphing structures. Soft Matter, 16(33), 7739-7750.
[2] Hafner, C., & Bickel, B. (2021). The design space of plane elastic curves. ACM Trans Graphics (TOG), 40(4), 1-20.