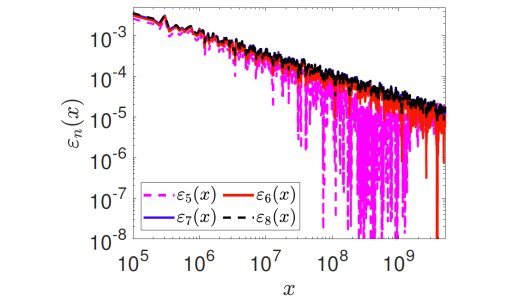
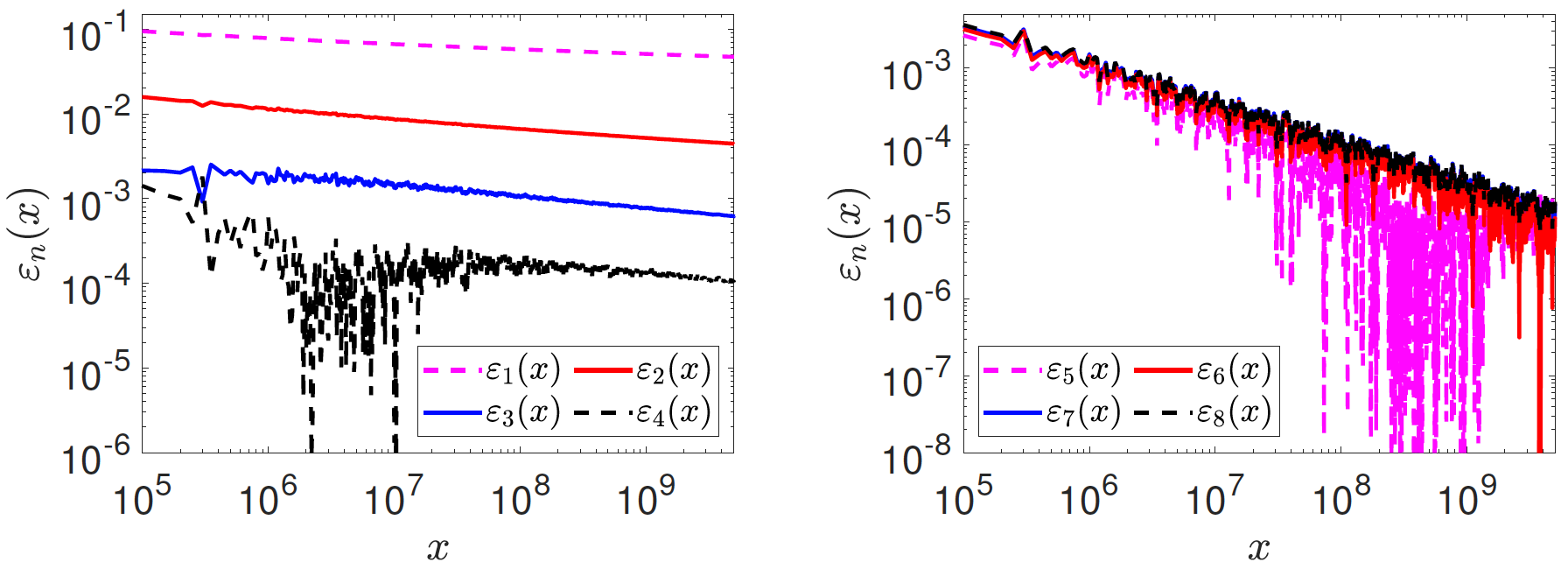
Define the prime-counting function $\pi(x)$ to be the number of natural primes less than or equal to $x$. One of the forms of the celebrated prime number theorem gives an asymptotic expansion for the prime-counting function as $$ \pi(x) \sim \frac{x}{\log x} \sum_{n=0}^\infty \frac{n!}{(\log x)^n} $$ This means that, truncating at any order $N$, we obtain the 'best asymptotic approximation' up to that order as $$ \pi(x) = \alpha_N(x) + o\left( \frac{x}{(\log x)^{N}} \right) $$ where $$\alpha_N(x) = \frac{x}{\log x} \sum_{n=0}^{N-1} \frac{n!}{(\log x)^n} $$ is the approximation of $\pi(x)$ up to the $N$-th term. In order to visualise the behaviour of this approximation, we define the relative errors: $$\varepsilon_{N}(x) = \frac{\left|\pi(x) - \alpha_N(x) \right|}{\pi(x)}$$ and plot them in the figure below.
The left panel shows relative errors $\varepsilon_N(x)$, for $N=1$, $2$, $3$ and $4$, as a function of $x$. We use a log-log plot to illustrate that these approximations are indeed relatively accurate, although the behaviour of $\varepsilon_N(x)$ includes some irregular components. The right panel shows relative errors $\varepsilon_N(x)$, for $N=5$, $6$, $7$ and $8$, as a function of $x$, visualized again using a log-log plot.
Now, let $\pi_2(x)$ be the number of integers less than or equal $x$ which can be written as the product of two prime factors. Such numbers are sometimes called semiprimes. In their recent paper, Oxford Mathematicians Dragos Crisan and Radek Erban study the asymptotic behaviour of the function $\pi_2(x)$, which has asymptotic expansion $$ {\hskip 5cm} \pi_2 (x) \sim \sum_{n=1}^{\infty} (n-1)! \, \frac{x \log(\log x)}{(\log x)^n} + \sum_{n=1}^{\infty} C_{n-1} \, \frac{x}{(\log x)^n} {\hskip 5cm} (*) $$ where $C_0$, $C_1$, $C_2$, $C_3,$ $\dots$, are real constants that can be calculated explicitly. Observe that the expansion $(*)$ is very similar to the one involved in the prime number theorem. The main difference is that the expansion $(*)$ involves two types of terms, one type containing the extra factor $\log(\log x)$. These results can be obtained by only using 'elementary methods' (such as one of Landau's original counting lemmas) and the prime number theorem, without appealing to complex analytic methods. Moreover, it turns out that $C_0 = M$, the Meissel-Mertens constant, defined by $$ M := \lim_{x\rightarrow \infty} \left( \sum_{p\leq x} \, \frac{1}{p} \, - \, \log (\log x) \right) = 0.26149721284764278 \dots $$ The constants $C_n$, for $n=1,2,3,\dots$, can be written in terms of weighted sums of constants $B_n$, which are, in some sense, similarly defined to the Meissel-Mertens constant, by: $$ \sum_{p\leq x} \frac{(\log p)^n}{p} = \frac{(\log x)^n}{n} + B_n + \mathcal{O}\! \left( e^{-\sqrt[14]{\log x}} \right). $$
The natural question to ask is how good an approximation equation $(*)$ gives. Plotting the graphs of the relative errors gives pictures similar to the ones above. They can be found here. This shows that the function $\pi_2(x)$ and its associated asymptotic series are natural generalisations of $\pi(x)$ and the prime number theorem. In fact, similar counting functions can be considered more generally. Defining $\pi_k(x)$ to be the number of integers less than or equal $x$ which can be written as the product of $k$ prime factors, its asymptotic series is given by $$\pi_k(x) \sim \frac{x}{\log x}\,\sum_{n=0}^{\infty}\frac{P_{n,k} (\log (\log x))}{(\log x)^n} \,,$$ where $P_{n,k}$ are polynomials of degree $k-1$ and with leading coefficient equal to $n!/(k-1)!$.
Photo of Radek Erban (after photo of Dragos) by Ian Wallman.