Much of theoretical physics is built on the concept of perturbation theory. Essentially perturbation theory is the idea that we can find a small quantity in the physical system we wish to describe and use that to expand the equations describing the system. In this way we obtain a simpler set of equations to solve.
In high energy physics we are concerned with the fundamental constituents of nature and their interactions, so this small parameter is usually the coupling constant, which determines the strength of the interaction between particles. In other words, a small coupling constant means weak interactions, so the particles only exert very little force on one another.
Perturbation theory is a powerful tool that has produced a remarkable amount of insight in just about every area of theoretical physics. Nonetheless, as you might expect, it is not always the case that a small quantity is available in the problem we wish to describe. And this is where the trouble starts...In theoretical physics, non-perturbative is synonymous with difficult. In fact this challenge encompasses a substantial sector of quantum field theory (QFT), which we refer to as strongly-coupled. Strongly-coupled QFTs are actually common-place. A central piece of the standard model, namely QCD, the theory of quarks, is an example. And here perturbation theory is utterly helpless. Frankly, these sectors of QFT could contain just about anything!
In short, the situation is this: a comprehensive understanding of strongly-coupled QFTs presents a formidable challenge in theoretical physics, which has clearly proven to lie well beyond the scope of conventional methods. So in order to make progress on this problem we must find fundamentally new approaches, and sharper, more sophisticated tools. The line of attack that I have chosen in my research, is to apply one of the most elegant and extensive frameworks at our disposal, namely string theory.
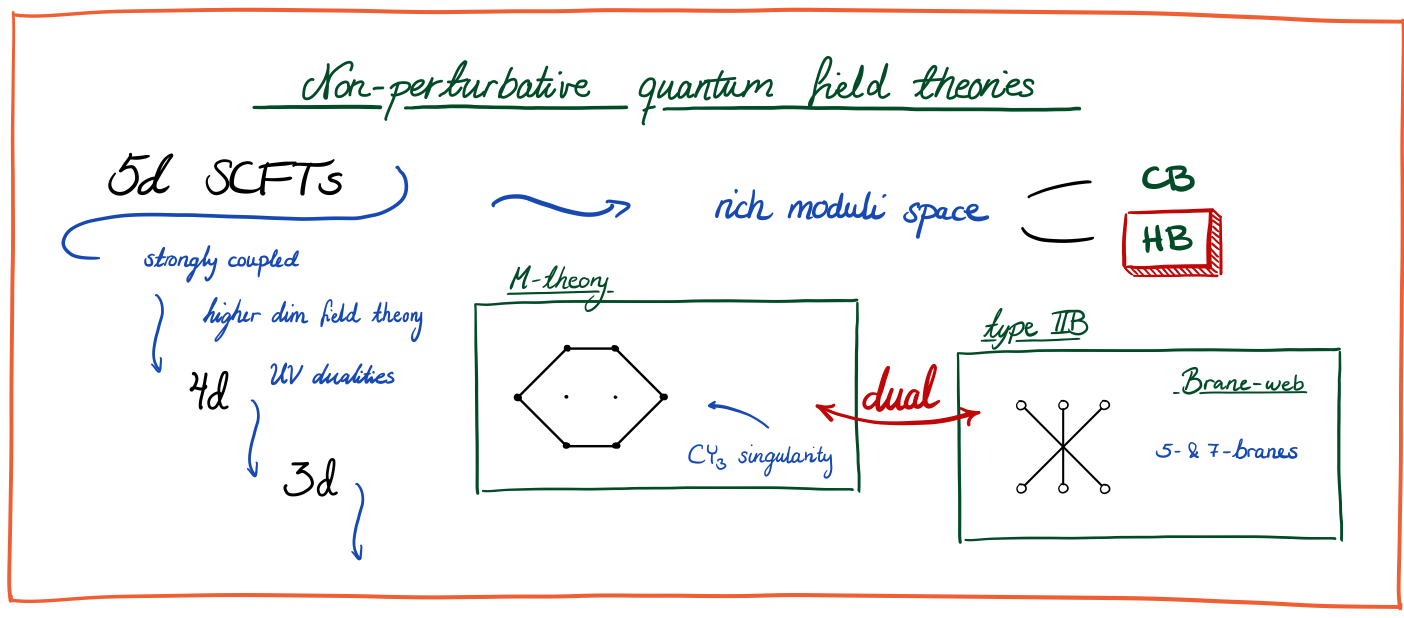
String theory provides a very high level of control and yet is flexible enough that it has recently been employed to construct and study strongly-coupled QFTs that were previously either entirely opaque or not even known to exist! Moreover, it is a higher-dimensional theory (10 dimensional to be precise - or 11 if you include M-theory) which might strike you as a weakness, or at the very least a redundancy of the theory, but that is not so for the purpose at hand. This is because physicists have understood how to compactify string theory on a manifold to realise QFTs of any lower dimension. And this is precisely what supplies the versatility to build a plethora of non-perturbative QFTs with one overarching organisational principle: the choice of compactification manifold.
In fact, the advantage of this higher-dimensional point of view goes even beyond that and here is how: just as we can consider lower-dimensional systems, like systems that live on a plane in space rather than 3d, we can in principle also ask about the behaviour of QFTs in 4 or 5 spatial dimensions. Even though these theories are clearly not something we run into in a laboratory, they might teach us about new aspects of QFT (as indeed they have already) which I personally consider plenty motivation to study them. A priori we might well expect these theories, that live in different dimensionalities, to have nothing whatsoever to do with one another. But far from this being the case, they are in fact all connected through compactifications!
Say I build a 4+1d QFT in string theory with some particular set of fundamental particles and specified interactions between them. Then it might occur to me to further reduce this theory on a torus or a general Riemann surface, and then make the surface small enough that we do not regard it as an extended dimension. In this way I have obtained a new 2+1d QFT whose matter and interactions will depend on the data of the 'parent' 4+1d QFT and the properties of the Riemann surface.
So far, this way of thinking has already delivered abundant new types of QFTs, rich with new symmetries, dynamics and phases to discover. And the powerful machinery of string theory gives us access to many of the salient features of these theories. To name (drop) a few: string dualities, such as T-duality between type IIA and type IIB string theory, relate geometric constructions of QFTs to brane-webs (see here and here for more), and Mirror Symmetry descends to relations between (the moduli space of) QFTs (see here for more). Yet the richness of this landscape leaves so much more to explore, and we have much work ahead of us before a complete picture, connecting many if not all(!) QFTs is truly within view.
Figure above adapted from a conference poster. Marieke Van Beest is a postgraduate student in Oxford Mathematics.