Quantum field theory (QFT) is a natural language for describing quantum physics that obeys special relativity. A modern perspective on QFT is provided by the renormalization group (RG) flow, which is a path defined on the coupling constant space and evolves from the ultraviolet (UV) to the infrared (IR) fixed point. In particular, the theories on the IR fixed point are scale-invariant and most of them are known to be promoted to a conformal field theory (CFT).
There are enormous motivations for studying the CFT. CFT has been utilized to understand the condensed matter phenomena such as the second-order phase transition or the fractional quantum Hall effect. CFT has also received attention from string theorists, due to its connection to quantum gravity via AdS/CFT correspondence. Furthermore, some aspects of CFT are closely related to number theory. For instance, there is unexpected relation between the torus partition function of the chiral $c=24$ two-dimensional CFT and the Monster group, the largest sporadic group [1]. This striking connection is referred to as the moonshine phenomena and has recently been studied extensively.
The power of conformal symmetry enables us to explore the non-perturbative aspects of the QFT. One recent trend in theoretical physics is to analyze the constraint of symmetry. More precisely, the conformal symmetry almost determines the structure of the four-point correlation function, and the crossing symmetry of the four-point correlation function leads us to the universal constraints on the spectrum and operator product expansion coefficients. This technique is called the 'conformal bootstrap' [2], and this subject is actively studied here in the Oxford Mathematical Physics Group.
Modular bootstrap: In my research, I applied the idea of the 'bootstrap technique' to the two-dimensional CFT to understand the non-perturbative perspectives of QFT in two-dimensional spacetime. In two-dimensional spacetime, the conformal symmetry is enhanced to the Virasoro symmetry. Furthermore, if I put the two-dimensional CFT on the torus, the genus-one surface, then the observable of CFT is regarded as the modular form of a certain weight. For instance, the torus partition function is a weight zero modular form as it should be invariant under the modular transformation.
One goal of my research is to explore the space of two-dimensional CFTs based on the 'modular bootstrap program'. Since the two-dimensional CFTs are governed by the Virasoro symmetry, the torus partition function can be decomposed by the Virasoro characters $\chi_h(\tau)$ as follows.
\begin{align}
\begin{split}
&Z(\tau, \bar{\tau}) = \chi_0(\tau) \bar{\chi}_0(\bar{\tau}) + \sum_{h,\bar{h}} d_{h,\bar{h}}\chi_h(\tau) \bar{\chi}_{\bar{h}}(\bar{\tau}) + \sum_{n \in \mathbb{Z}} d_{n} \left( \chi_0(\tau) \bar{\chi}_{\bar{h}}(\bar{\tau}) + \text{c.c.} \right) \\
\end{split}
\end{align}
Here $d_{h,\bar{h}}$ and $d_{n}$ are degeneracy, they are theory-dependent quantity. The Virasoro symmetry cannot tell us further details such as the spectrum and degeneracy. However, the modular invariance can tell us something! Indeed, the following 'modular bootstrap equation',
\begin{align}
Z(\tau, \bar{\tau}) = Z(\gamma \tau, \gamma \bar{\tau}), \qquad \gamma \in SL(2,\mathbb{Z}),
\end{align}
reveals new constraints on the spectrum and degeneracy. In the following paragraphs, I introduce two representative works of mine that solved the modular bootstrap equation.
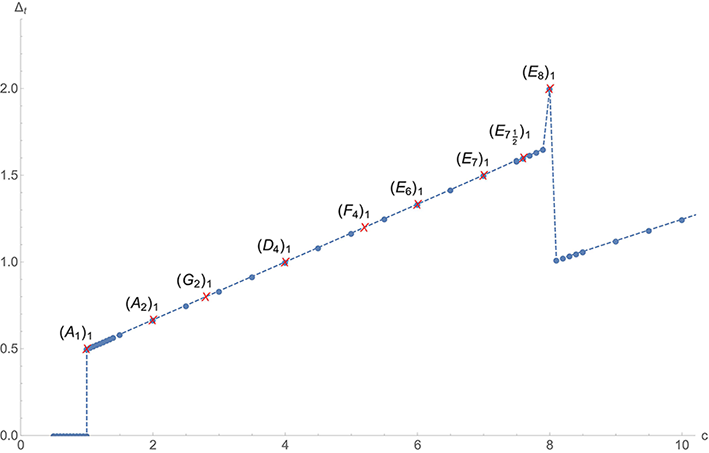
Figure 1: Numerical upper bound on the twist gap $t = \Delta - |j|$ for the non-current operators in the presence of holomorphic currents. Two-dimensional CFTs are 'not' allowed to exist when the twist gap is above the numerical boundary. It turns out that certain rational CFTs appear on the numerical boundary. They are level-one Wess-Zumino-Witten models with Deligne-Cvitanović exceptional group.
Numerical bootstrap: It is not easy to solve the modular bootstrap equation explicitly since the torus partition function receives contributions from the infinitely many Virasoro primaries. There have been many trials to find the solutions to the modular bootstrap equation. One of my previous works adapted numerical techniques like semi-definite programming to analyze the modular constraint [3]. The result is summarized in Figure 1 above. The $x$-axis and $y$-axis stand for the central charge and a gap in the twist (difference between a conformal dimension and spin), respectively. The result implies that the two-dimensional CFTs with large twist gaps are not allowed to exist.
Analytic bootstrap: Hans Rademacher proposed a beautiful idea for solving the modular bootstrap equation for the holomorphic function [4]. Suppose the modular form of our interest has the following structure.
\begin{align}
J(\tau) = \frac{1}{q} + \sum_{n=1}^{\infty} a_n q^n, \qquad q = e^{2\pi i \tau}
\end{align}
From the modular constraints $J(\gamma\tau) = J(\tau)$, Rademacher showed that the Fourier coefficients are expressed by the infinite sum
\begin{align}
a_n = \sum_{s=1,2,\cdots} K(-n,1,s) \frac{2\pi}{\sqrt{n} s} I_1\left( \frac{4\sqrt{n}\pi}{s} \right),
\end{align}
where $K(a,b,s)$ is the Kloosterman sum and $I_1(x)$ is the modified Bessel function. One can show that the above sum converges to the integer and recovers the famous $J$-invariant!
\begin{align}
J(\tau) = \frac{1}{q} + 196884 q + 21493760 q^2 + \cdots
\end{align}
There have been debates on the existence of three-dimensional pure quantum gravity in AdS space. In work with Luis Fernando Alday [5], we aim to explore the three-dimensional pure quantum gravity in the eye of the modular bootstrap program. The spectrum of quantum gravity is discretized and the degeneracy is a positive integer. Therefore, the partition function of boundary two-dimensional CFT is expected to satisfy the additional conditions such as positivity, integrality, and discreteness. We extend Rademacher's techniques to find non-holomorphic solutions to the modular bootstrap equation. Our new solution is a weight-zero modular form; however, it violates the positivity and discreteness like the Poincaré series [6,7]. Our result may imply the non-existence of a single two-dimensional CFT mapped to the three-dimensional pure quantum gravity. Indeed, no weight-zero modular forms satisfying positivity, integrality, and discreteness were discovered until now. I believe that the understanding of the space of the non-holomorphic modular form will provide us with a strong hint on the problem of three-dimensional pure quantum gravity.
Jin-Beom Bae is a Postdoctoral Research Associate in Oxford Mathematics.
References:
[1] I. B. Frenkel, J. Lepowsky, A. Meurman, “A natural representation of the Fischer-Griess Monster with the modular function J as character,” Proceedings of the National Academy of Sciences 81 (10) (1984) 3256–3260.
[2] D. Poland, and D. Simmons-Duffin, "The conformal bootstrap", Nature Phys 12, 535–539 (2016).
[3] J.-B. Bae, S. Lee, J. Song, “Modular Constraints on Conformal Field Theories with Currents,” JHEP 12 (2017) 045.
[4] H. Rademacher, “The Fourier Coefficients of the Modular Invariant J(τ ),”, American Journal of Mathematics 60, no. 2 (1938), 501-512.
[5] L. F. Alday, J.-B. Bae, “Rademacher Expansions and the Spectrum of 2d CFT,” JHEP 11 (2020) 134.
[6] A. Maloney, E. Witten, “Quantum Gravity Partition Functions in Three Dimensions,” JHEP 02 (2010), 029.
[7] N. Benjamin, H. Ooguri, S. H. Shao and Y. Wang, “Light-cone modular bootstrap and pure gravity,” Phys. Rev. D 100 (2019) no.6, 066029.


