N is for Networks

Renaud Lambiotte is a Professor of Networks and Nonlinear Systems and Turing Fellow of Somerville College.

They have worked in different aspects of network science, most prominently in community detection, and more recently in temporal networks and higher-order networks.

This open access book (http://networksciencebook.com/) provides a gentle introduction to several concepts of network science, and is written by the father of the “preferential attachment model”.

This online platform (https://www.complexity-explorables.org/fields/network-science/) allows users to explore visually different models for network formation via numerical simulations.

Many systems are composed of elements in interaction and can be represented by networks. Think of Facebook, of course, and its millions of users interconnected by friendship relations; Wikipedia, where different pages are connected by hyperlinks; and ecosystems, where different types of species may depend on each other. In each case, the system can be seen as a set of nodes for the entities and of edges that represent their pairwise interactions. The study of graphs is not in itself a new field of research, and they have been studied for decades in different  areas of Mathematics, as they naturally appear in problems involving discrete systems and their connectivity. Take the problem of matchmaking pairs of people based on their preferences or their similarity, or of optimising the route of a travelling salesperson, or the famous 4-colour map theorem. Network science, as it is often called today, differs from these traditional questions, because of its strong empirical basis and because of the question at its core: How does the structure of a network affect its functioning? In the Facebook example, this general question could give: How does the  structure of the social graph affect the propagation of fake news in society? This philosophy is nicely illustrated in a seminal paper by the applied mathematicians Duncan Watts and Steven Strogatz, in which they explored empirical data and uncovered that different  types of networks, from different domains, exhibit a similar combination of order and disorder, leading to there being surprisingly many triangles (three nodes that are all connected), together with short-cuts that tend to make the graph “small” (a feature often called the six degrees of separation after the earlier works of the social scientist Stanley Milgram). But the work of Watts and Strogatz did not stop at this empirical observation: they also proposed a simple network model interpolating between a lattice (a highly structured graph where certain motifs are repeated) and a random graph to reproduce their empirical findings, and explored how the presence of random short-cuts affects dynamics. In their case, they originally considered a system where an oscillator would be assigned on each node, and they studied the emergence of collective synchronisation depending on the underlying coupling structure. 

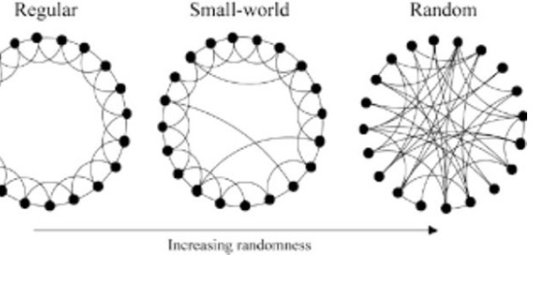
Small-world networks combine local regularity and random short-cuts. 

Network science builds on different  areas of Mathematics. A graph can be encoded by a matrix, a square array of numbers that captures all the key information about the graph, enabling us to use ideas and tools from linear algebra, such as eigenvalues and eigenvectors, to understand structural and dynamical properties of the graph. A famous example of this is Google’s PageRank, which is defined as the dominant eigenvector of the normalised graph Laplacian (a particular matrix associated with the graph) and which historically was used by Google to rank webpages by their importance. Network science also heavily relies on statistics, as it is grounded in empirical observations, and it is thus critical to understand how errors impact the results of network algorithms. Dynamical systems is another central component and in fact network science has also influenced research in the dynamics of interacting systems.

What is particularly powerful in networks is their generality, as very different systems can be represented by the same abstraction. Social networks and metabolic networks can be represented and analysed by the same tools, even if the nature of their nodes and edges are very different. Moreover, networks have the advantage of combining two desirable properties. They are often sparse, as nodes are usually connected to a tiny fraction of the total number of nodes when the system is sufficiently large (think how many friends you have relative to the world population). Yet they allow for connectivity via indirect paths between pairs of nodes, as an idea or a virus may spread from neighbour to neighbour across the system. A particularly important line of research deals with the design of efficient algorithms to extract information from the myriad of connections of large networks. In the Wikipedia example, this can help to create a classification of sciences based on the structure of the hyperlinks alone. A wide variety of algorithms have been proposed to help comprehend the unusual geometry of networks, for instance to measure the importance of nodes, to find groups of nodes that play a similar role, or to predict the future creation of edges in temporal networks.  Currently, promising lines of research include the interface between networks and machine learning, for instance through the concept of graph neural networks, and the possibility to extend network methods to more general relational structures, such as hypergraphs. Most importantly, network thinking has now permeated different domains of science and engineering, providing a common language, and emphasising their connections in a way that, circularly, calls for a network representation.

References: 
Watts, Duncan J., and Steven H. Strogatz. "Collective dynamics of ‘small-world’ networks." Nature 393.6684 (1998): 440-442