One of the current challenges in computational neuroscience is to understand how a huge number of interacting neurons can generate and sustain complex patterned activities that play important roles in the functioning of the brain. Because biologically plausible models of single neurons are far too complex to be tackled numerically or analytically, neuroscientists have proposed simpler, self-contained models aimed at encompassing the qualitative complexity of neural networks in a tractable framework.
The main idea of these models is often to consider a finite collection of N neurons evolving and interacting in time through simplified rules and then to let the number N tend to a theoretical infinity. This limit yield models for the behaviour of a randomly chosen cell in a large neural network, a procedure called 'mean field approximations'. These mean-field models are often written in the form of stochastic differential equations or partial differential equations.
This general approach has fostered an understanding of the so-called grid cells. Grid cells are a particular type of neuron which play a pivotal role in the navigational system of mammals. Since their discovery in 2005, their functioning has been extensively studied. It is believed that they allow the brain to store and integrate information about its spatial environment by generating a specific hexagonal firing pattern. Yet many questions remain about how grid cells generate this patterned activity, how they are connected to each other and to other brain areas, and how their activity is affected by random fluctuations (noise) in the network.
Recently, a partial differential equation of Fokker-Planck type describing modules of grid cells was obtained through the aforementioned mean-field aproximation procedure by José Antonio Carrillo, Andrea Clini and Susanne Solem [1]. Numerical simulations and analytical study of the linearisation was performed by José Antonio Carrillo, Helge Holden and Susanne Solem [2].
Their preliminary results suggested that the characteristic hexagonal pattern can be understood as a phase transition from the flat activity state when the neuronal noise decreases below a threshold value. José Antonio Carrillo, Susanne Solem and myself, Pierre Roux, [3], have used general tools from bifurcation theory, namely the Crandal-Rabinowitz theorem, to relate rigorously the apparition of patterned activity to the Fourier modes of the connectivity function and the value of the noise. With this theory, we can easily produce graphs showing, in terms of the connectivity function’s Fourier decomposition, for which values of the noise there is a bifurcation from the flat activity state (see Figure 1).
Each intersection of the blue curve with a horizontal line (Fourier modes) is such a bifurcation. It appears that the first four bifurcations contain all the necessary harmonics to make a hexagonal pattern. Our numerical simulations show fast convergence of any solution of the model to this hexagonal firing pattern (see Figure 2). We have also started an ongoing study of other mathematical properties of this model: abstract existence of solutions, a priori bounds and asymptotic stability of the stationary states.
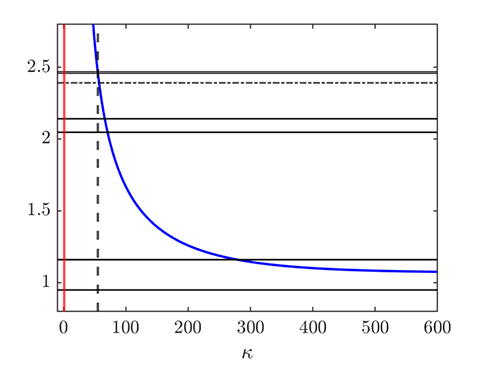
Figure 1 : Bifurcation points are represented as the crossing of Fourier modes (the black horizontal lines) and a characteristic curve as a function of the inverse of the noise strength (the blue line).

Figure 2 : Time-transient patterns of the partial differential equation with noise strength close to the first three bifurcation points. From top left to bottom right, moving horizontally, snapshots at t = 40 ms, 220 ms, 1500 ms, 1810 ms, 2190 ms and 2400 ms.
[1] J. A. Carrillo, A. Clini, S. Solem. The mean field limit of stochastic differential equation systems modelling grid cells, arXiv preprint, arXiv:2109.07936, 2021
[2] J. A. Carrillo, H. Holden, S. Solem. Noise-driven bifurcations in a neural field system modelling networks of grid cells, Journal of Mathematical Biology, accepted
[3] J. A. Carrillo, P. Roux, S. Solem. Noise-driven bifurcations in a nonlinear Fokker-Planck system describing stochastic neural fields, arXiv preprint, arXiv:2205.11968, 2022


