Algebraic topology is the study of the continuous shape of spaces by the discrete means of algebra. The beginning of modern algebraic topology can be traced back to an insight of Pontryagin in the 1930s which relates the global smooth geometry of manifolds to algebraic invariants associated to the local symmetries of those manifolds - this relation converts something smooth and geometric (called a manifold, potentially endowed with further structure) to something algebraic that can be written down with symbols and formulas, i.e. something that a computer could understand ... in principle at least!
In practice, unfortunately, there is not always an algorithmic method to go from the smooth-geometric side to the symbolic-algebraic side. The lack of an algorithmic method here can be traced to fundamental problems with the classical non-computational approach to manifolds and continuous spaces themselves: for instance, no computer programme can list all manifolds, nor can it recognize when a given space is a manifold, nor can it recognize when two given manifolds are in fact the same up to some natural equivalence.
These obstructions to computability in the theory of manifolds are unfortunate for various reasons; for instance, they imply that certain problems in mathematical physics are not solvable by a computer. But the obstructions feel as unexpected and unnatural as they are unavoidable: didn't Pontryagin establish a relation between the geometric theory of manifolds and some symbolic algebraic theory? And isn't symbolic algebra something computers can do? While we cannot magically wish away the problems of computers understanding the classical theory of manifolds, this line of questioning does nonetheless lead us onto an interesting and novel path: can we, from the symbolic-algebraic side of Pontryagin's translation, reverse-engineer a new geometric theory of manifolds that does not suffer from the same fundamental problems as the classical theory?
The question is, in fact, best approached from the yet more abstract perspective of higher category theory. Higher category theory initially arose as a branch of algebraic topology in the 1960s, but soon after (upon realising the theory's broader role in studying "general mathematical structure") it became its own independent field of study. Higher category theory, in some sense, generalizes the traditional notion of spaces: while in a traditional space, any path is "invertible", i.e. it can be travelled in both directions, in a higher category this need not be the case; paths can be "one-way" paths, i.e. they can be travelled in one direction only. This, initially, seems to make the idea of what spaces are more difficult to work with. But the opposite turns out to be the case: by allowing paths to be one-way, we cut down the complexity of our theory because we need not specify the mathematical structure that makes paths invertible (these invertibility structures have, in fact, quite complicated behaviour).
This idea of a higher-categorical perspective on Pontryagin's insight has been known to experts for a while (at least since the 1990s), leading, for instance, to the formulation of the influential "tangle and cobordism hypotheses" which relate the topology of manifolds and the algebra of higher categories [1]. Following this line of research, work began towards the study of algebraicizable (and thereby computerizable) types of geometric objects underpinning manifold theory. These geometric objects have been referred to by several names - we like to call them manifold diagrams for their joint role as being geometric objects comprising of manifolds and as being diagrams representing algebraic compositions.
The idea of manifold diagrams builds on a long history of other "diagrammatic-algebraic notions", starting as early as Sir Roger Penrose's diagrammatic notation for tensor calculus in the 1970s. Formally giving a definition of manifold diagrams turned out to be a difficult feat, as manifold diagrams ought to (a) behave like an algebraic object that can be composed by diagrams in the sense of higher category theory while (b) nonetheless also admitting a purely geometric description. The challenge of unifying these two aspects of the desired definition meant that, in the decades that followed their initial informal conception, formalizations of manifold diagrams where only achieved in dimensions 3 and less.
In recent work, Oxford Mathematicians Christoph Dorn (right, picture above) and Christopher Douglas (left) built a novel theory of "one-way spaces" called framed spaces that is precisely tailored to the purposes of higher-dimensional computer algebra. The core aspects of this theory are spelled out in their book, "Framed combinatorial topology" [2, 4]. The theory of framed combinatorial topology allows them to finally define the geometric notion of manifold diagram in all dimensions: that definition and its implications are discussed in their recent research monograph "Manifold diagrams and tame tangles" [3]. That monograph also shows that is possible to reintroduce invertible structure for paths, resulting in a variation of the notion of manifold diagrams called "tame tangles"; this notion formalizes a computable version of the objects central to the aforementioned tangle hypothesis. They conjectured that many of the previous obstructions to computability questions about manifolds may, in fact, be resolved when working with tame tangles.
Let us briefly sketch the simple underlying idea of framed spaces and manifold diagrams. It may be worth starting with a description of "dimensions of space" in the following intuitive form.
- In 1-dimensional space, one may move (forwards and backwards) only in one direction. Think, for instance, of ants walking forward and backwards on a wire.
- In 2-dimensional space, one may move in two directions: think, for instance, of ants walking on a plate. A central new phenomenon in dimension 2, is that our ants may move around the plate in a circle, returning to their starting point without visiting any point on their route twice.
- In 3-dimensional space, one may now move in three directions: at this point, we give our ants wings, and let them fly above the plate. To understand the relation to two dimensions, imagine that the mid-day sun projects the ants' shadow onto the plate (see Fig. 1): the 3-dimensional movement is fully described if, in addition to observing the 2-dimensional movement of the ants' shadows on the plate, we also measure their altitude above the plate. Three dimensions again brings new phenomena: flying ants can now move in "circular" paths that trace out knots (see Fig. 2).
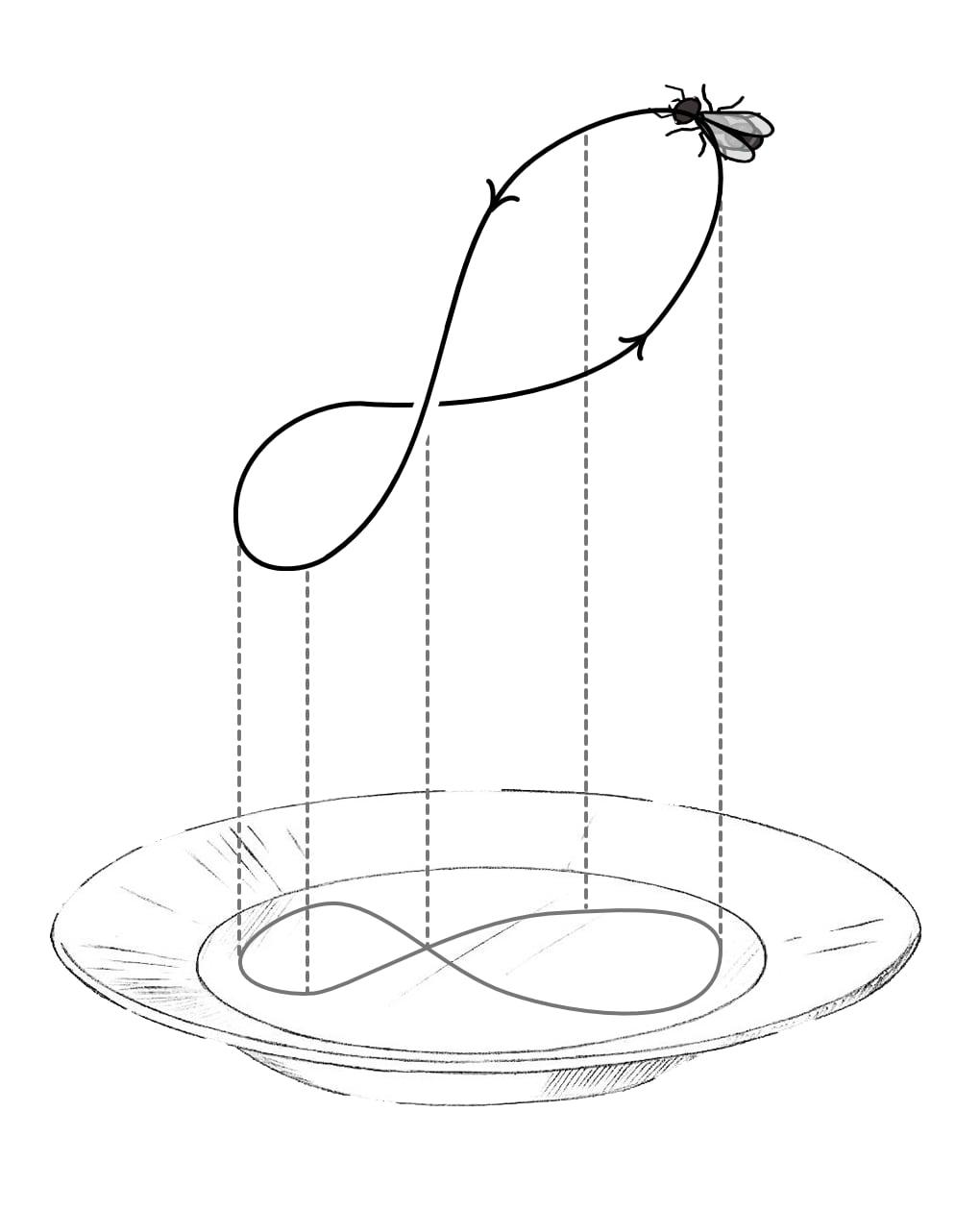
Figure 1: a 3-dimensional movement and its 2-dimensional projection.
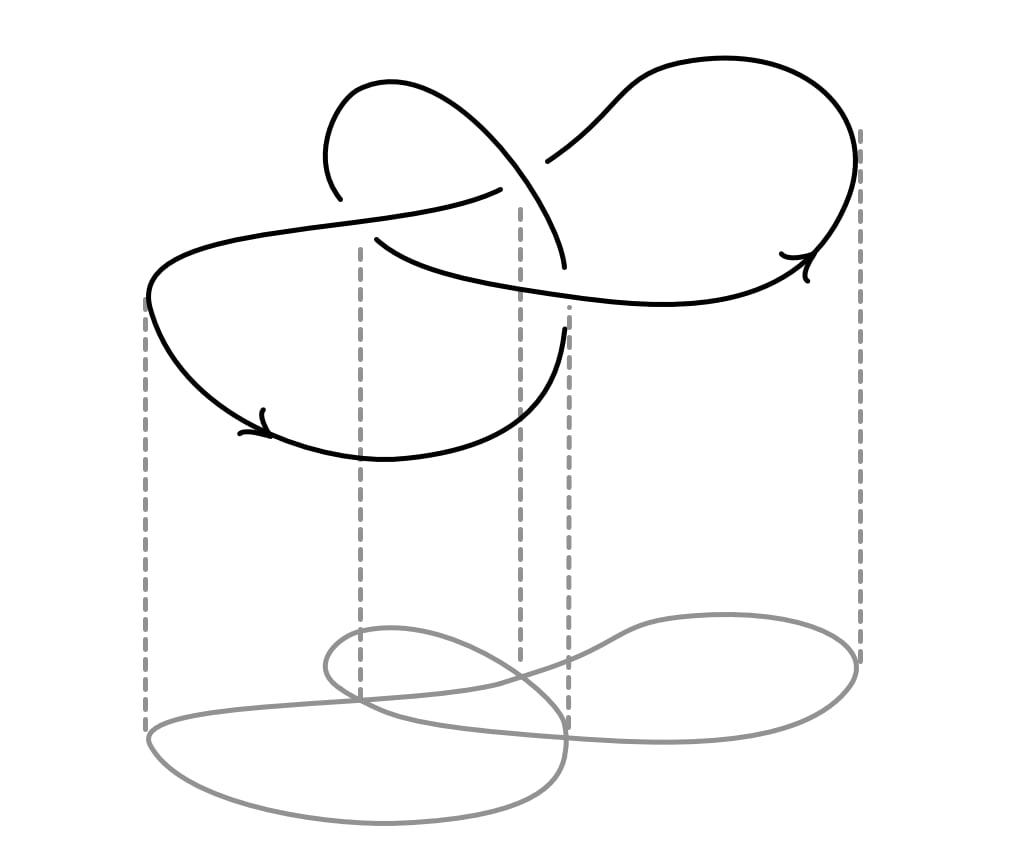
Figure 2: A knotted circle, and its projection to the 2-dimensional plane.
An elementary, but fundamental observation, is that there is no need to stop the process at this point: dimension is just a number. We can continue the above sequence of dimensions: just as 3-dimensional movement was described by 2-dimensional movement together with an altitude number, 4-dimensional movement is 3-dimensional movement together with another "altitude" number - ie. there is a 3-dimensional movement that is the projection of the 4-dimensional movement, and at each point we add a number for the "(4-th dimensional) altitude" at that point. We can continue in this way to understand n-dimensional movement for any number n. Higher dimensions bring fascinating and often mysterious new types of phenomena (starting, for instance, with the knotting of circles in dimension 3, mentioned above), and algebraic topologists have spent much time understanding these phenomena and describing their patterns across dimensions.
The idea of n-dimensional framed space is a simple variation of the above step-by-step procedure: instead of allowing ants to both increase and decrease their altitudes, we only ever allow them to increase their altitudes, thereby choosing a preferred direction of travel. Initially this approach seems very restrictive: how can an ant fly in a circle if it is only allowed to go up? In fact, the circular process can still be described, but when considering one-way travel we must refine our view by "breaking up" the movement into two phases: the semi-circle on which the ant is moving up will have to be separated from the semi-circle on which it is moving down, and the latter half will be replaced by a semi-circle of a "time-reversed ant" that is traveling up as well (see Fig. 3).

Figure 3: Breaking up a circular movement into two upwards movements, one of which is given the label 'time reversed'.
In manifold diagrams, all manifolds need to be broken into pieces in this way. As it turns out, studying the basic shapes of these pieces, called framed regular cells, is what makes the computerization of manifold diagrams possible. A formal definition of manifold diagrams then reads as follows: a manifold diagram is a framed conical stratification of framed Euclidean space that can be broken up into finitely many framed regular cells.
In many ways, framed spaces are easier to understand and better behaved than their traditional counterparts: ultimately, this can be traced back to the fact that the theory of framed spaces clearly separates the concept of space from the concept of invertibility. One example of the good behaviour of manifold diagrams is, for instance, that manifold diagrams satisfy a local form of the so-called Hauptvermutung or "main conjecture" (which asks about the uniqueness of combinatorial descriptions of spaces, and is known to be false in the classical context!); another example of good behaviour in the new framework of framed spaces is the observation that we can computationally decide when two given manifold diagrams are framed equivalent [2]. These behaviours become particularly useful when studying the aforementioned high-dimensional algebraic-topological phenomena (such as knotted higher-dimensional spheres). Indeed, from the perspective of framed spaces these phenomena will be broken up into smaller pieces, and importantly, the process of creating these decompositions is always unambiguous (a result that is called the "existence of unique coarsest refining meshes" [2]).
The mechanism for producing such canonical decompositions then allows us to study the "elementary" pieces of algebraic-topological phenomena. Studying such pieces, for instance, leads us to higher-dimensional generalizations of braids and of the Reidemeister moves of traditional knot theory. A subset of these elementary pieces provides a computable, combinatorial viewpoint on singularities of manifolds; unlike the classical theory of singularities which suffers from intractable infinite-dimensional moduli problems, the framed-space view on singularities conjecturally leads to a discrete, finite classification [3] (see Fig. 4). In summary, in the theory of framed spaces one obtains a novel, computable perspective on classical questions about both algebraic-topological and geometric-topological phenomena.
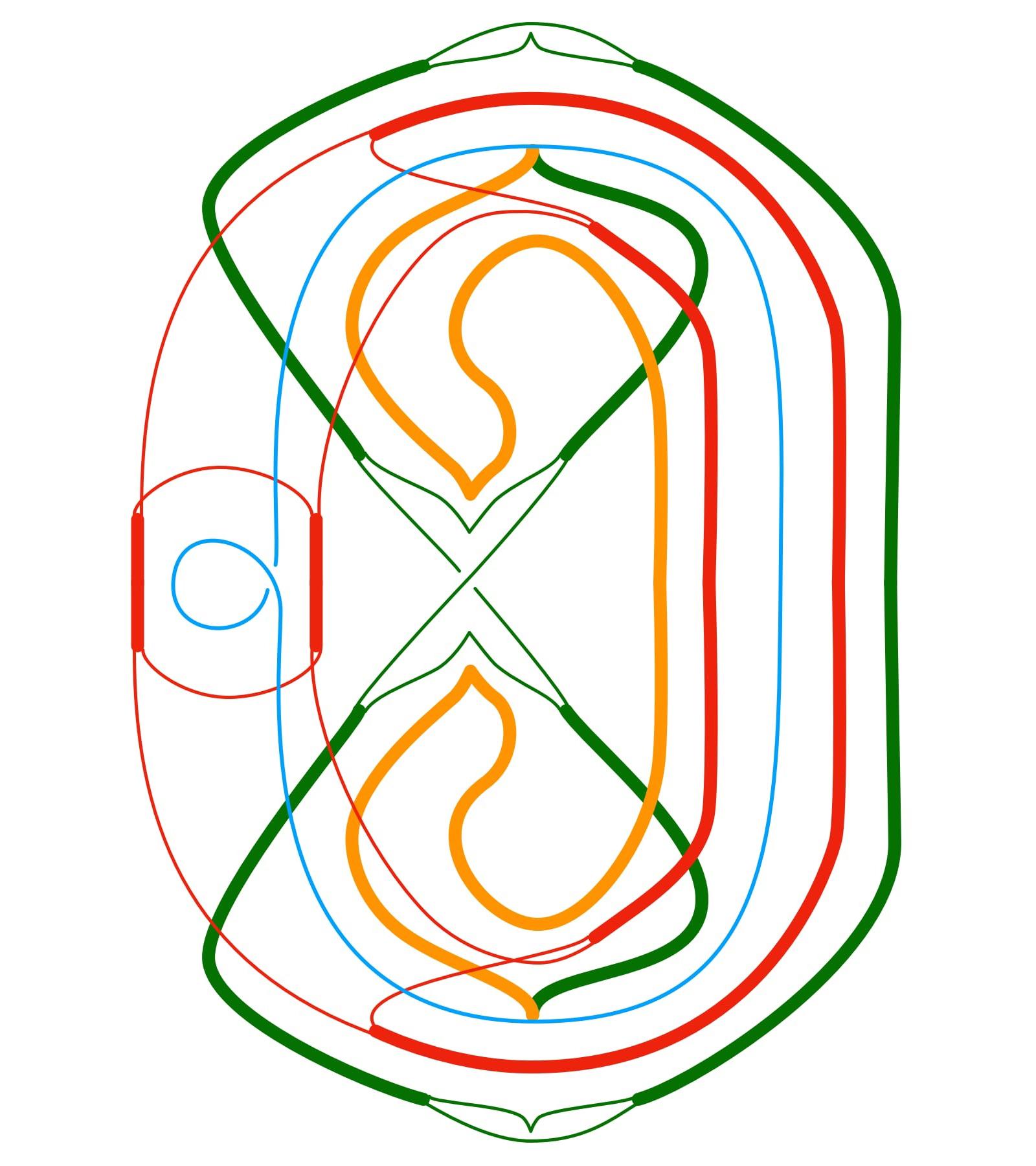
Figure 4: The D4 singularity in framed space (illustrated by projecting its critical submanifolds to the 2-dimensional plane).
Let us end this short overview on a more philosophical note: why is it useful to have manifolds stand on computable foundations in the first place? One implicit motivation comes from mathematical physics, and the emerging belief that the laws of fundamental physics are, ultimately, of information-theoretic nature (whether based on a quantum or classical or other form of computational paradigm). Given that the geometric toolset of modern algebraic topology has become increasingly important in the mathematical study of fundamental physics, one long-term aim of this line of research is to show that the algebraic structures of higher category theory provide a powerful alternative approach to describing the geometric nature of our world, without leaving the realm of computable foundations.
References:
[1] J. Baez and J. Dolan, Higher-dimensional Algebra and Topological Quantum Field Theory, Journal of Mathematical Physics 1995
[2] C. Dorn and C. Douglas, Framed combinatorial topology, arXiv 2021
[3] C. Dorn and C. Douglas, Manifold diagrams and tame tangles, arXiv 2022
[4] C. Dorn and C. Douglas, A brief introduction to framed combinatorial topology


