In 1900, David Hilbert posed his list of 23 mathematical problems. While some of them have been resolved in subsequent years, a few of his challenging questions remain unanswered to this day. One of them is Hilbert's 16th problem, which asks questions about the number of limit cycles that a system of ordinary differential equations can have. Such equations appear in modelling real-world systems in biological, chemical or physical applications, where their solutions are functions of time. A limit cycle is a special periodic solution, a solution which (after a certain period of time) returns back to the state where it started. Hilbert's 16th problem considers ordinary differential equations (ODEs) which can be written in the following form
\begin{eqnarray*} \frac{\mbox{d}x}{\mbox{d}t} & = & f(x,y), \\ \frac{\mbox{d}y}{\mbox{d}t} & = & g(x,y), \end{eqnarray*}
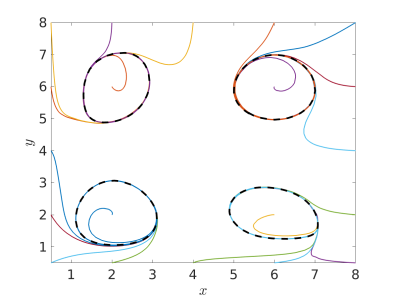
where $f(x,y)$ and $g(x,y)$ are polynomials. The solutions of such equations are two functions of time, $x(t)$ and $y(t)$, and they can be plotted in the $x$--$y$ plane as shown in the picture above which has four limit cycles. In this example these four limit cycles are plotted using the black dashed lines as the four closed curves. If a solution of the ODEs starts at any point on these curves, it returns back to the starting point after a finite time. Moreover, the above picture also includes some other solutions of the same ODEs, which are plotted using different colours. Some of them start on the boundary of our plot and some of them start inside the limit cycles. In all cases, the plotted solutions approach one of the limit cycles. This means that the solutions of the ODEs are following one of the four periodic regimes, provided that we observe the system for a sufficiently long time, or, as mathematicians would say, the presented limit cycles are stable.
The example above has been constructed using the approach developed in the recent paper by Oxford Mathematician Radek Erban and his collaborator Hye-Won Kang from University of Maryland. In their paper, they investigate limit cycles in chemical systems. Some of them are described by ODEs in the form above, so any limit cycles found in such chemical systems are directly relevant to Hilbert's 16th problem. However, there are also other classes of chemical systems which correspond to a more general set of differential equations, with applications to modern 21st century scientific fields, like synthetic biology or DNA computing. Clearly, David Hilbert could not have had these applications in mind when he formulated his problems in 1900, so what is the exact connection?
Hilbert's 16th problem asks questions for the ODEs written above, where $f(x,y)$ and $g(x,y)$ are real polynomials of degree at most $n$. Denoting $H(n)$ the maximum number of limit cycles for such systems, neither the value of $H(n)$ (for $n \ge 2$) nor any upper bound on $H(n)$ have yet been found. Chemical systems directly corresponding to Hilbert's 16th problem are chemical systems with two chemical species which can be described by the ODEs in the form above. In particular, if we denote by $C(n)$ the maximum number of stable limit cycles in such chemical systems, then we have $C(n) \le H(n)$. In the paper, a lower bound for $C(n)$ is proven, which directly implies a lower bound on Hilbert's number $H(n)$.
However, from the point of view of applications to mathematical chemistry, it would be too restrictive to consider systems with only two chemical species. Therefore, the authors' paper also studies more general systems with $N>2$ chemical species. In fact, if David Hilbert lived today, he could formulate his 16th problem for systems of $N \ge 2$ ordinary differential equations with polynomial right-hand sides and he would not only pose very challenging open mathematical problems, but their solutions would also have a wider impact on applications. In the paper, chemical systems with $K$ limit cycles are constructed, where $K$ can be arbitrarily large. In addition to their ODE models mentioned above, chemical systems can also be modelled by a more detailed stochastic description, written as continuous time discrete space Markov chains and simulated by the Gillespie algorithm. Stochastic models can help us to investigate the likelihood that the chemical system will follow one of its limit cycles.