Systems of chemical reactions figure prominently in models throughout the natural sciences. Biology in particular gives rise to hugely complicated reaction networks which, somehow, perform intricate and delicate functions. How do we make sense of these complex networks, and try to understand the relationships between their structure and function?
One approach is to look for “motifs” – smaller subnetworks appearing in the large networks, which are easier to study and understand. We may get to these simpler networks by ignoring some species or reactions; or by collapsing chains of reactions into a single reaction, for example. But this leads to the question: can we be sure that the larger network will necessarily inherit interesting behaviours of the smaller network we derived from it? The answers are not obvious: there are interesting examples which show that some very natural enlargements of a reaction network can actually destroy nontrivial behaviours in the smaller network.
One strand of my recent work has focussed on making this question precise and finding some answers. With various collaborators I have now proved a large number of results, using the machinery of perturbation theory, which tell us which network enlargements preserve interesting behaviours in reaction networks, including multistationarity, oscillation, and bifurcations. Some simple examples of such enlargements are in Figure 1. The results are constructive: they also tell us roughly for which parameter values we should expect these behaviours in the larger network. They have been used to predict the occurrence of behaviours in large reaction networks without recourse to simulation.
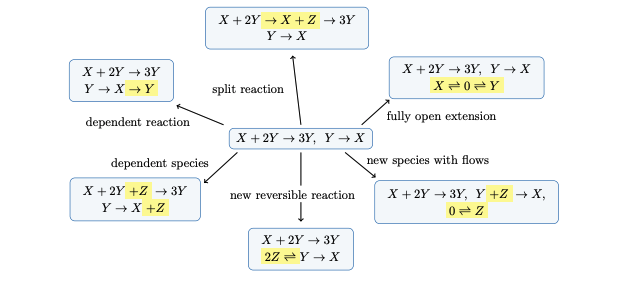
Figure 1: Some simple examples of enlargements which have been proven to preserve nondegenerate dynamical behaviours in reaction networks. The small network in the centre is easily shown to admit nondegenerate multistationarity; surrounding it are six enlargements of this network, created by splitting reactions of the central network, or adding to it new reactions and species. In each case, general theorems tell us that the enlarged network must admit nondegenerate multistationarity. Similar claims can be made about other behaviours such as oscillation and, indeed, bifurcations, in enlarged networks.
Murad Banaji is Departmental Lecturer in Applied Mathematics in Oxford
Some of his papers on these themes include:
[BBH23] M. Banaji, B. Boros and J. Hofbauer, The inheritance of local bifurcations in mass action networks, arXiv preprint.
[BB23] M. Banaji and B. Boros, The smallest bimolecular mass action reaction networks admitting Andronov-Hopf bifurcation, Nonlinearity 36(2) (2023) 13981433.
[Ban23] M. Banaji, Splitting reactions preserves nondegenerate behaviours in chemical reaction networks (2023), SIAM J Appl Math 83(2) (2023).
[BBH22] M. Banaji, B. Boros and J. Hofbauer, Adding species to chemical reaction networks: preserving rank preserves nondegenerate behaviours, Applied Math Comput 426 (2022) p127109.
[Ban20] M. Banaji, Building Oscillatory Chemical Reaction Networks by Adding Reversible Reactions, SIAM J Appl Math 80(4) (2020) 17511777.
[BP18] M. Banaji and C. Pantea, The inheritance of nondegenerate multistationarity in chemical reaction networks, SIAM J Appl Math 78(2) (2018) 11051130.
[Ban18] M. Banaji, Inheritance of oscillation in chemical reaction networks, Applied Math Comput 325 (2018) 191209.


