In this case study I report on a collaboration with Mo Dick Wong (Durham University), in the area of analytic and probabilistic number theory. We studied questions on a random model for the Möbius $\mu$ function. This function is one of the most elusive functions in number theory, and encodes deep questions on primes. Let's define it properly.

It is a multiplicative function defined on the positive integers, meaning $\mu(nm)=\mu(n)\mu(m)$ holds if $n$ and $m$ have no common factors, so it suffices to define $\mu$ at prime powers. On primes, it is defined as $\mu(p)=-1$, and on proper prime powers it is defined to be $0$. Its first $10$ values are \[ 1, -1, -1, 0, -1, 1, -1, 0, 0, 1.\] This function is interesting because the Riemann Hypothesis, originally a statement about the location of the zeros of the Riemann zeta function $\zeta(s)=\sum_{n\ge 1}n^{-s}$, or equivalently on estimates for the number of prime numbers up to $x$, can be formulated as follows: the sum $\sum_{n \le x} \mu(n)$ of values of $\mu$ exhibits square-root cancellation, in the sense that $|\sum_{n \le x} \mu(n)|$ grows slower than $x^{\frac{1}{2}+\varepsilon}$ for each $\varepsilon>0$. As this conjecture holds the key to properties of primes and $\zeta$, it is not expected to admit a simple resolution... 

The conjectural square-root cancellation in $\sum_{n \le x} \mu(n)$ is often motivated by an analogy with random walks: if $(X_n)_{n=1}^{\infty}$ are i.i.d. random variables taking the values $-1,+1$ with probability $\frac{1}{2}$, then the random walk $\sum_{n\le x} X_n$ can be shown to be $O(x^{\frac{1}{2}+\varepsilon})$ almost surely. To connect with number theory, one often encounters the saying that the 'Möbius values $(\mu(n))_{n=1}^{\infty}$ behave like independent coin tosses'. This is not accurate for two reasons: $\mu$ is a deterministic function (no randomness is involved), and it is multiplicative, so values at composite integers are determined by values at prime powers. 

Wintner [15], in 1944, had the idea of defining random multiplicative functions (rmf-s), for which these probabilistic considerations can be, to some extent, justified. He defined the Rademacher rmf $\beta$ as follows: the values at primes, $(\beta(p))_{p \text{ prime}}$, are i.i.d. random variables taking the values $-1$ and $+1$ with probability $1/2$, $\beta(n) = \prod_{p \mid n} \beta(p)$ if $n$ is a product of distinct primes, and $\beta(n)=0$ if $n$ has a repeated prime factor. In particular, $\beta(n)=0$ if and only if $\mu(n)=0$. He proved unconditionally that one has square-root cancellation, that is, given $\varepsilon>0$, $|\sum_{n\le x} \beta(n)| = O(x^{\frac{1}{2}+\varepsilon})$ holds almost surely. A slightly different function is the Steinhaus rmf $\alpha$ defined as follows: the values at primes, $(\alpha(p))_{p \text{ prime}}$, are i.i.d. random variables following the uniform distribution on $\{ z \in \mathbb{C}: |z|=1\}$ and $\alpha(n) = \prod_{p \mid n} \alpha(p)^{a_p}$ if $n=\prod p^{a_p}$ is composite. 

Various works in recent years were dedicated to the study of the distribution of $\sum_{n\le x} \alpha(n)f(n)$ and $\sum_{n\le x} \beta(n)f(n)$ for certain (deterministic) weights $f$. Together with my collaborator Mo Dick Wong, we proved new results on such sums when $f$ is a multiplicative function satisfying technical conditions [3]. Before stating our main result, we mention the two motivations for studying such sums: 

• (Direct motivation) The behaviour of $\sum_{n \le x} \alpha(n)f(n)$ sheds light on the statistical behaviour of classical number-theoretic sums such as $\sum_{n\le x} n^{it} f(n)$ and $\sum_{n \le x} \mu(n)n^{it} f(n)$ ($t$ chosen randomly) or $\sum_{n \le x} \chi(n) f(n)$ ($\chi$ a Dirichlet character chosen randomly).
• (Indirect motivation) The study of $\sum_{n \le x} \alpha(n)f(n)$ leads to interesting probabilistic considerations, due to the lack of independence among the different terms in the sum. 

To convince the reader, we mention that in the context of the first motivation, Harper [5] initially proved that $\mathbb{E}|\sum_{n\le x} \alpha(n)|=o(\sqrt{x})$ holds, resolving a conjecture of Helson. Then, in subsequent work, he was able to show that $T^{-1}\int_{0}^{T}|\sum_{n\le x} n^{it}|dt=o(\sqrt{x})$ if $\min\{x,T/x\} \to \infty$ [6], by making use of his work on $\alpha$. Put differently, proving results for $\alpha(n)$ is a stepping stone for proving corresponding results on $n^{it}$ or $\chi(n)$. 

In the context of the second motivation, we now know that the behaviour of these sums relates to an area in probability theory called Gaussian multiplicative Chaos, see especially [5] (cf. [13]); this has opened up new directions in number theory and probability, and informed the collective understanding of the Riemann zeta function. 

In previous works by other authors [7, 4, 1, 2, 11, 12, 9, 8, 14], it was established that for various choice of $f$, the random variable \[ S_{x,f}:=\frac{1}{(\sum_{n \le x}|f(n)|^2)^{1/2}}\sum_{n \le x} \alpha(n) f(n)\] tends in distribution to a complex Gaussian distribution. Unfortunately, in the most natural case, $f\equiv 1$, the sum $\sum_{n \le x} \alpha(n)$ is far from being fully understood, but see [5] for the study of its low moments (cf. [13]) which implies $S_{x,1}$ tends to $0$ in distribution. 

In our joint work [3], we have proved that for a wide class of multiplicative functions $f$, $S_{x,f}$ has a non-trivial non-Gaussian limiting distribution. Our proof uses a martingale approach, pioneered by Harper [4], and crucially builds on a proof structure introduced by Najnudel, Paquette and Simm in a related problem in random matrix theory [10]. Some examples of $f$ to which our result applies include

• If we fix $q \in \mathbb{N}$ and a subset of reduced residues $S$ modulo $q$ such that $|S| < \phi(q)/2$, then one can take $f$ to be the indicator of products of primes congruent modulo $q$ to a residue in $S$. E.g., we can take $f$ to be the indicator of all integers composed only of primes $\equiv 1 \bmod 5$. 
• $f(n)=d_z(n)$, $f(n)=z^{\Omega(n)}$ and $f(n)=z^{\omega(n)}$, as long as $|z|^2 \in (0,1/2)$. Here $d_z$ is the $z$-th divisor function, $\Omega(n) = \sum_{p^k \mid n} 1$ and $\omega(n) = \sum_{p \mid n}1$. 

In more detail, we end up showing that $S_{x,f}$ tends in distribution to \[ \sqrt{V_{\infty}} \cdot G\] where $G \sim \mathcal{N}_{\mathbb{C}}(0,1)$ is independent of $V_{\infty}$. The random variable $V_{\infty}$ is an integral defined using a random measure $m_{\infty}(dt)$: \[ V_{\infty}:=\frac{1}{2\pi} \int_{\mathbb{R}} \frac{m_{\infty}(dt)}{|1/2+it|^2}.\] This random measure is constructed as a limit: \[m_{\infty}(dt) = \lim_{x \to \infty} m_{x,\infty} (dt), \qquad m_{x,\infty}(dt)=\frac{|\sum_{P(n)\le x}\alpha(n)f(n)n^{-1/2-it}|^2}{\mathbb{E} |\sum_{P(n)\le x}\alpha(n)f(n)n^{-1/2-it}|^2}dt.\] The measure $m_{x,\infty}(dt)$ has appeared in the literature in a special case, see Harper [5].

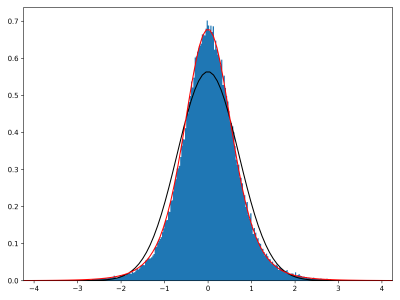
While this might all sound abstract, one can plot the histogram of $S_{x,f}$ and compare against (approximations of) the proven limiting distribution. Take $f(n) := 0.7^{\Omega(n)}$ for instance. The figure above shows the empirical distribution of $\Re S_{x,f}$ (blue). The black curve corresponds to the Gaussian density with matching 2nd moment, whereas the red curve corresponds to the (empirical) distribution of $\sqrt{\frac{1}{2\pi} \int_{\mathbb{R}} \frac{m_{x, \infty}(dt)}{|\frac{1}{2} + it|^2}} \Re(G)$ where $\Re(G) \sim \mathcal{N}(0, 1/2)$ is independent. Despite the modest size of $x = 10000$, the red curve produces a surprisingly good fit.

Ofir Gorodetsky is a postdoctoral research associate in Oxford Mathematics.

[1] D. Aggarwal, U. Subedi, W. Verreault, A. Zaman, and C. Zheng. Sums of random multiplicative functions over function fields with few irreducible factors. Math. Proc. Camb. Philos. Soc., 173(3):715– 726, 2022. 

[2] S. Chatterjee and K. Soundararajan. Random multiplicative functions in short intervals. Int. Math. Res. Not., 2012(3):479–492, 2012. 

[3] O. Gorodetsky and M. D. Wong. Martingale central limit theorem for random multiplicative functions, 2024.

[4] A. J. Harper. On the limit distributions of some sums of a random multiplicative function. J. Reine Angew. Math., 678:95–124, 2013. 

[5] A. J. Harper. Moments of random multiplicative functions. I: Low moments, better than squareroot cancellation, and critical multiplicative chaos. Forum Math. Pi, 8:95, 2020. Id/No e1. 

[6] A. J. Harper. The typical size of character and zeta sums is o( √ x), 2023. 

[7] B. Hough. Summation of a random multiplicative function on numbers having few prime factors. Math. Proc. Camb. Philos. Soc., 150(2):193–214, 2011. 

[8] O. Klurman, I. D. Shkredov, and M. W. Xu. On the random Chowla conjecture. Geom. Funct. Anal., 33(3):749–777, 2023. 

[9] J. Najnudel. On consecutive values of random completely multiplicative functions. Electron. J. Probab., 25:28, 2020. Id/No 59. 

[10] J. Najnudel, E. Paquette, and N. Simm. Secular coefficients and the holomorphic multiplicative chaos. Ann. Probab., 51(4):1193–1248, 2023. 

[11] M. Pandey, V. Y. Wang, and M. W. Xu. Partial sums of typical multiplicative functions over short moving intervals. Algebra Number Theory, 18(2):389–408, 2024. 

[12] K. Soundararajan and M. W. Xu. Central limit theorems for random multiplicative functions. J. Anal. Math., 151(1):343–374, 2023. 

[13] K. Soundararajan and A. Zaman. A model problem for multiplicative chaos in number theory. Enseign. Math. (2), 68(3-4):307–340, 2022. 

[14] V. Y. Wang and M. W. Xu. Paucity phenomena for polynomial products, 2024. 

[15] A. Wintner. Random factorizations and Riemann’s hypothesis. Duke Math. J., 11:267–275, 1944.