I study the large scale geometry of infinite groups and spaces, focusing on quasi-isometries, which are maps between groups or spaces that preserve the large scale geometry. Since quasi-isometries need not be continuous, distinguishing groups up to quasi-isometries can be challenging. This motivates considering invariants, that is, properties preserved under quasi-isometries.
An important example of such an invariant is the Dehn function. For a finitely presented group $G$ arising as the fundamental group of a compact CW complex $X$, the Dehn function of $G$ can be both interpreted geometrically as an isoperimetric function of the universal cover $\tilde{X}$ of $X$, and combinatorially, as the number of relations one needs to apply to show that a word of a given length represents the trivial element.
Intuitively, we can define the Dehn function of $G$ as the function $\delta_G \colon \mathbb{N} \to \mathbb{N}$ such that \[ \delta_G(n) = \max \{ \mathrm{FillingArea}(\lambda) \mid \lambda \colon S^1 \to \tilde{X} \ \text{loop of length} \ n \}, \] where $\mathrm{FillingArea}(\lambda)$ can informally be defined as the minimal number of $2$–cells in $\tilde X$ that must be crossed in a null-homotopy of $\lambda$ in the $2$–skeleton of $\tilde X$. Alternatively, it is the minimal area enclosed by an extension of $\lambda$ into the disc. Thus, the Dehn function can be regarded as a homotopical filling function.
This can be illustrated pictorially as follows:

| 
|
The Dehn function is not a single function, but an equivalence class of functions with the same growth rate, making it a well-defined invariant. The appropriate notion of equivalence is as follows: two functions $f,g \colon \mathbb{N} \to \mathbb{N}$ are $\asymp$-equivalent, and we write $f\asymp g$, if $f\preccurlyeq g$ and $g\preccurlyeq f$, where $f \preccurlyeq g$ means that there exists a constant $C>0$ such that \[ f(n) \leq Cg(Cn +C) + Cn +C \] for all $n \geq 0$.
Determining the exact Dehn function requires matching upper and lower bounds, which can be quite challenging.
A key feature of the Dehn function is that it captures hyperbolicity: a group $G$ is hyperbolic if and only if its Dehn function is linear; in symbols $\delta_G(n) \asymp n$. Moreover, if a group $G$ is not hyperbolic, then its Dehn function must grow at least as fast as a polynomial of degree $2$, that is, $n^2 \preccurlyeq \delta_G(n)$.
In recent joint work with Yu-Chan Chang and Matteo Migliorini, we obtained the first complete classification of the Dehn functions of finitely presented Bestvina-Brady groups [CGMM25].
In 1997, Bestvina and Brady introduced a class of groups linking topology and finiteness properties of groups [BB97]. To each simplicial graph $\Gamma$, they associated a group $\mathit{BB}_\Gamma$ , whose finiteness properties depend on the homotopy type of the flag complex $\Delta(\Gamma)$, where simplices correspond to cliques of $\Gamma$.
The Dehn functions of finitely presented Bestvina–Brady groups have been extensively studied, see for instance [ABD+13, DERY09, CF17]. One general result was obtained by Dison, who proved that the Dehn function of a finitely presented Bestvina-Brady group is bounded above by a polynomial of degree $4$ [Dis08].
Building on this previous work, we showed that the Dehn function of every finitely presented Bestvina-Brady group is always a linear, quadratic, cubic, or quartic polynomial. In fact, we gave a fairly simple criterion on the defining graph $\Gamma$ that determines the degree of the polynomial. Before stating this, let me give a few examples.
Example 1 . It is known that $\mathit{BB}_\Gamma$ is hyperbolic if and only if $\Gamma$ is a tree. In particular, this characterises all the graphs $\Gamma$ for which the Dehn function of $\mathit{BB}_\Gamma$ grows like a linear polynomial.
Recall that the join of two subgraphs $\Gamma_1$ and $\Gamma_2$ is a graph $\Gamma_1 * \Gamma_2$ formed by taking the (disjoint) union of the two graphs and connecting with an edge between every vertex of $\Gamma_1$ to every vertex of $\Gamma_2$. A graph $\Gamma$ is called reducible if it is a join $\Gamma_1 \ast \Gamma_2$, where $\Gamma_1$ and $\Gamma_2$ are nonempty subgraphs, else it is called irreducible.
Example 2 . Suppose $\Gamma$ is a cone graph, i.e., the join of a finite simplicial graph $\Lambda$ and a single vertex $c$. In this case it can be seen that $\mathit{BB}_\Gamma$ is isomorphic to the right-angled Artin group $\mathit{A}_\Lambda$. Right-angled Artin groups are $\mathrm{CAT}(0)$ groups, a notion of non-positive curvature. In particular, this implies that their Dehn functions are bounded above by a quadratic polynomial [Bri02, Theorem 6.2.1]. Since in this case the group $\mathit{BB}_\Gamma$ is not hyperbolic, it contains $\mathbb{Z}^2$ as a subgroup, so its Dehn function actually grows like a quadratic polynomial.
Example 3. If $\Gamma$ can be expressed as the join of three or more non-empty subgraphs, then the Dehn function of $\mathit{BB}_\Gamma$ grows like a quadratic polynomial [CF17].
Examples of a cone graph and a graph which is the join of three nonempty graphs are illustrated in the following pictures:
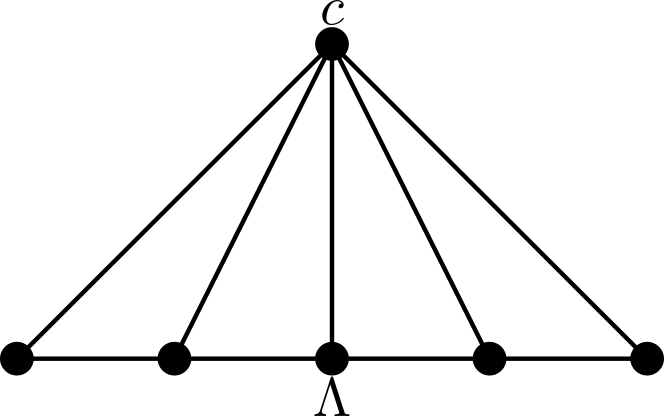
where $\Lambda$ is the path of length $4$.
| 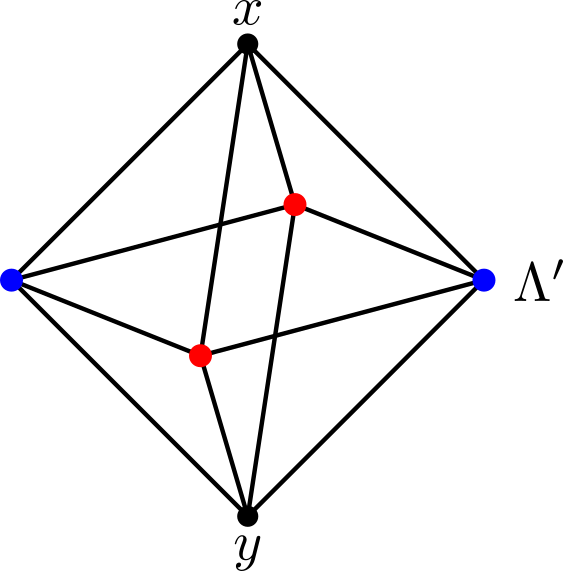
and two graphs in $\Lambda'$ each consisting of a pair of non-adjacent vertices (red and blue, respectively). |
Inspired by Example 2 and Example 3 we defined the following.
Definition 1 (Essentially 2-reducible graph). A graph is called essentially 2-reducible if it is a join of two irreducible subgraphs, each with at least two vertices; equivalently, if it is neither a cone graph nor a join of three or more subgraphs.
An example of an essentially 2-reducible graph is illustrated in Figure 3; while examples of graphs that are not essentially 2-reducible are depicted in Figure 1 and Figure 2.
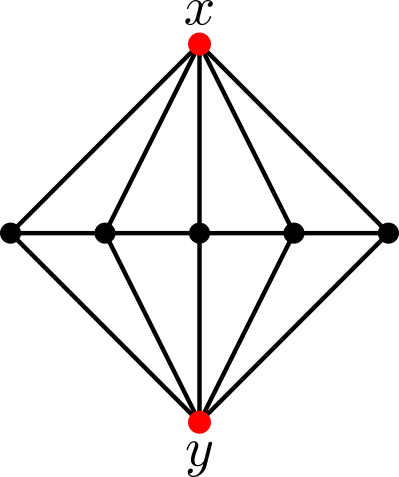
join of the graph on vertices $\{x,y\}$ and the path of length $4$. | 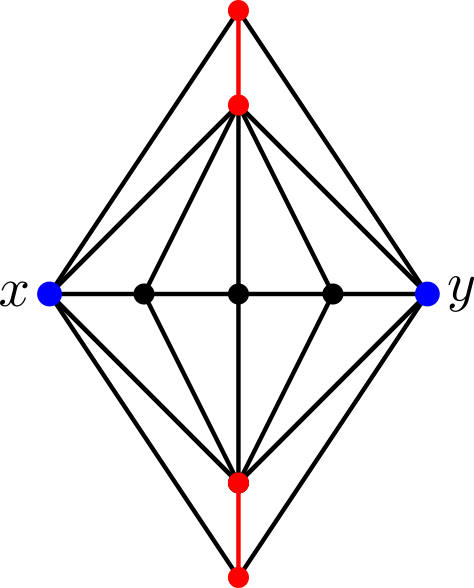
(see Definition 2 below): the join of the red subgraph and the blue subgraph $\{x, y\}$ is a maximal reducible subgraph whose flag complex is not simply connected. |
For general graphs, the situation is harder, but essentially 2-reducible graphs are central to understanding the Dehn functions of Bestvina-Brady groups. By examining the maximal reducible subgraphs of $\Gamma$, that is, reducible subgraphs that are maximal with respect to inclusion among all reducible subgraphs of $\Gamma$, we fully characterise the Dehn function of $\mathit{BB}_\Gamma$. To state this full characterisation, we introduced the following definition.
Definition 2. Let $\Gamma$ be a finite simplicial graph whose associated flag complex $\Delta(\Gamma)$ is simply connected. If this is the case, we say that $\Gamma$ has property $(\mathcal D_1)$, and additionally, it has property
- $(\mathcal D_2)$ if $\Gamma$ is not a tree;
- $(\mathcal D_3)$ if $\Gamma$ contains a maximal reducible subgraph that is essentially 2-reducible;
- $(\mathcal D_4)$ if $\Gamma$ contains a maximal reducible subgraph whose associated flag complex is not simply connected.
We are now ready to state the characterisation of the Dehn functions of Bestvina-Brady groups that we obtained.
Theorem ([CGMM25]). Let $\Gamma$ be a finite simplicial graph such that the associated flag complex $\Delta(\Gamma)$ is simply connected. Let $d(\Gamma)$ be the maximal $\alpha \in \{1,2,3,4\} $ such that $\Gamma$ has property $(\mathcal D_\alpha)$. Then the Dehn function of the Bestvina-Brady group $\mathit{BB}_\Gamma$ satisfies \[ \delta_{\mathit{BB}_\Gamma}(n) \asymp n^{d(\Gamma)}. \]
The graph in Figure 3 has property $(\mathcal D_3)$ but it does not have property $(\mathcal D_4)$, so the Dehn function of the Bestvina-Brady group associated to it is cubic. The graph in Figure 4 has property $(\mathcal D_4)$, thus the Dehn function of the associated Bestvina-Brady group is quartic.
In conclusion, the Dehn function of $\mathit{BB}_\Gamma$ has only linear, quadratic, cubic, and quartic growth, and determining the exact Dehn function reduces to checking which of the properties $(\mathcal D_1)–(\mathcal D_4)$ the graph $\Gamma$ has.
References
| [ABD+13] | A. Abrams, N. Brady, P. Dani, M. Duchin, and R. Young. Pushing fillings in right-angled Artin groups. J. Lond. Math. Soc. (2), 87(3):663–688, 2013. |
| [BB97] | M. Bestvina and N. Brady. Morse theory and finiteness properties of groups. Invent. Math., 129(3):445–470, 1997. |
| [Bri02] | M. R. Bridson. The geometry of the word problem. Invitations to geometry and topology, Oxf. Grad. Texts Math., 7:29–91, 2002. |
| [CF17] | W. Carter and M. Forester. The Dehn functions of Stallings–Bieri groups. Mathematische Annalen, 368(1):671–683, June 2017. |
| [CGMM25] | Y.-C. Chang, J. García-Mejía, and M. Migliorini. Complete classification of the Dehn functions of Bestvina–Brady groups, July 2025. arXiv:2507.07566. |
| [DERY09] | W. Dison, M. Elder, Timothy R. Riley, and R. Young. The Dehn function of Stallings’ group. Geom. Funct. Anal., 19(2):406–422, 2009. |
| [Dis08] | W. Dison. An isoperimetric function for Bestvina-Brady groups. Bull. Lond. Math. Soc., 40(3):384–394, 2008. |
The original pictorial representations of the Euclidean plane and the hyperbolic disc are due to the Dutch artist M. C. Escher. These images are publicly available on wikiart.org under the Fair Use licence . The title of the works are (from left to right) Two Birds and Circle Limit IV (Heaven and Hell). These modifications were made by the author with nonprofit educational purposes.
Jerónimo García Mejía was a postdoctoral research associate in Oxford Mathematics where he is now an Academic Visitor.


