Einstein's equations describe how the curvature of spacetime relates to energy and mass. However, as analytical solutions are rarely feasible, numerical solutions of these equations on computers are indispensable and are crucial in modern astrophysics, such as the detection of gravitational waves. Despite successes, numerical simulations gradually lose accuracy in the long-term evolution of black holes, leading to non-physical predictions. This often stems from inappropriate reformulations and breaches of geometric constraints.
More specifically, Einstein's equations are a system of nonlinear geometric PDEs. In different coordinates, the equations describe the same physics but have rather different forms and properties. The gauge freedom (freedom of choosing coordinates) is a major challenge for discretising Einstein's equations. Moreover, 3+1 decompositions of Einstein's equations lead to several constraint equations, which are automatically satisfied in the time evolution at the continuous level. On the numerical level, violations of these constraints or the tensor symmetries (due to discretisation errors, for example) lead to significant instability. Therefore, addressing the challenges in the numerical computation of Einstein's equations involves choosing appropriate gauge conditions to reformulate the equations and designing numerical methods that preserve the tensor symmetries and constraint equations precisely.
The Einstein-Bianchi system is a well-posed first-order hyperbolic system with desirable mathematical properties [1, 2] and is a promising candidate for numerical discretisation. With a 3+1 decomposition, the linearised Einstein-Bianchi system reads \begin{equation}\tag{1} \begin{aligned} \dot{E}+\operatorname{curl}B=0,&\quad \operatorname{div}E=0,\\ \dot{B}-\operatorname{curl}E=0,&\quad\operatorname{div}B=0. \end{aligned} \end{equation} This system closely resembles Maxwell's equations. The key distinction is that, in (1), the unknowns $E$ and $B$ are transverse-traceless (TT; i.e., traceless, symmetric and divergence-free) tensor fields. In Maxwell's equations, no tensor symmetries are involved, and enforcing the constraint $\operatorname{div}B=0$ is feasible through a potential-based formulation with $A = \operatorname{curl}^{-1}B$. However, generalising this idea is not straightforward due to the TT nature of the tensors in (1). The development of numerical methods that precisely preserve the transverse–traceless conditions remains an ongoing challenge.
To overcome the difficulties associated with the strict transverse-traceless (TT) constraints, one may consider a relaxed formulation of the linearised Einstein-Bianchi system. Introducing a new variable $\sigma(t)=\int_0^t\operatorname{div}\operatorname{div}E\,\mathrm{d}s $, the linearised Einstein-Bianchi system (1) can be written as a Hodge wave equation with relaxed constraints, where $E$ and $B$ are either symmetric or traceless, but not both [7]: \begin{equation}\tag{2} \begin{aligned} \dot{\sigma} &= \operatorname{div}\operatorname{div}E,\\ \dot{E} & = -\operatorname{grad}\operatorname{grad}\sigma-\operatorname{sym}\operatorname{curl}B,\\ \dot{B} &= \operatorname{curl}E. \end{aligned} \end{equation} The above system (2) can be further reformulated as another Hodge wave equation [3]: \begin{equation}\tag{3} \begin{aligned} \dot{\sigma} &= \operatorname{div}\operatorname{div}E,\\ \dot{E} & = -\operatorname{dev}\operatorname{hess}\sigma-\operatorname{sym}\operatorname{curl}B,\\ \dot{B} &= \operatorname{sym}\operatorname{curl}E. \end{aligned} \end{equation} Now $E$ and $B$ are both symmetric and traceless tensors. Compared with the original form (1), these two Hodge wave formulations are more amenable to the design of stable discretisation methods. It should be noted, however, that neither (2) nor (3) can strongly preserve the divergence-free constraints.
My research focuses on developing structure-preserving finite element discretisations for the linearised Einstein-Bianchi system. The main idea is that, in order to obtain numerical stability, ensure convergence, and preserve key physical and geometric structures, it is important to recognise and discretise the underlying differential complexes and preserve the homological structures at the discrete level, rather than merely discretising individual spaces. Structures of different problems are encoded in different complexes. The finite elements for the Hodge wave equation (2) are closely related to the discretisation of two associated differential complexes, the so-called Hessian complex:
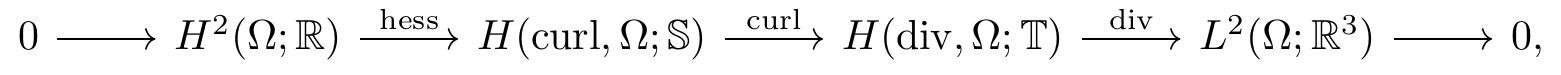
and the divdiv complex (which is dual to the Hessian complex):
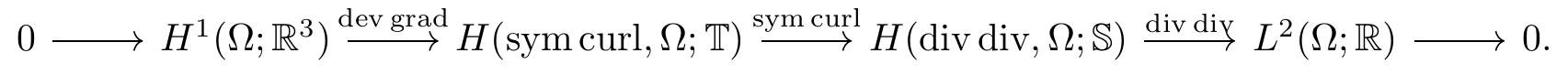
Here, $\mathbb{S}$ and $\mathbb{T}$ denote the space of symmetric and traceless tensors, respectively. The Hessian and divdiv complexes consist of Sobolev spaces with scalar-, vector-, or $\mathbb{S}$ ($\mathbb{T}$)-valued functions (for example, $H(\mathscr{D}, \Omega; \mathbb{S})$ is the space of $\mathbb{S}$ fields $u$ with $L^{2}$ coefficients such that $\mathscr{D} u$ is also in $L^{2}$). We have constructed the first family of conforming finite element spaces for the Hessian complex [4] and the divdiv complex [5, 6] in three dimensions with applications to the Hodge wave equation (2). This work offers new insights and techniques for designing novel finite elements for other differential complexes.
Compared with the Hodge wave equation (2), equation (3) preserves more of the intrinsic structure of the linearised Einstein–Bianchi system. It is also related to the conformal Hessian complex:
Meanwhile, the conforming finite element discretisation of the conformal Hessian complex is considerably more challenging. The main difficulties lie in the following aspects:
1. The geometric structure of the five-dimensional space $\mathbb{S}\cap\mathbb{T}$ is not well understood, which makes it difficult to characterise the bubble function spaces.
2. To ensure compatibility among finite element spaces, the construction typically involves high-order polynomials and super-smoothness, posing a significant barrier to practical computation.
Overcoming these challenges and developing computationally feasible numerical methods will be one of our primary research objectives.
Yizhou Liang is a postdoctoral research associate here in Oxford Mathematics.
References:
[1] Arlen Anderson, Yvonne Choquet-Bruhat, and James W. York, Jr. Einstein-Bianchi hyperbolic system for general relativity. volume 10, pages 353–373. 1997. Dedicated to Olga Ladyzhenskaya.


