Many systems that govern crucial aspects of our lives can be seen as interacting dynamical units. This includes systems on a vast variety of scales, from billions of tiny interacting neural cells that are a critical part of our brain to the large scale communication networks that keep our world running. While we may understand the behaviour of each dynamical unit, it is crucial to understand the emergent collective dynamics of all units together. Synchronisation is a prime example, where units behave in unison. Importantly, collective dynamics is related to function: for example, loss of brain synchrony is associated with neurological disease.
While the connectivity between units is traditionally assumed to be static, in many cases, it is natural to assume that connectivity between units adapts and changes over time. In the brain, changes of the connections between neural cells - also called plasticity - contributes to learning. In communication networks, we are staying connected while moving around. Hence, insights into the collective dynamics of such adaptive networks are critical in understanding, predicting, and designing the systems that govern our lives.
However, the analysis of dynamical networks where connections adapt suffers from the "curse of dimensionality": their complexity grows rapidly with an increasing number of units. That makes even small networks hard to understand: for example, a network of three nodes has six possible adaptive connections and adding one more node doubles that number to 12.
In our recent work, we developed dimension reduction techniques for adaptive networks by constraining the adaptive dynamics. Constraints mean, for example, that some network connections are kept fixed or there are relations between different links. For example, reciprocal links between two units could maintain the same value.
Constraints can be both intrinsic to the dynamics - they come from the adaptation rules themselves - or forced by a dynamical mechanism on a time scale distinct from the adaptation dynamics. Constraints come in different flavours, from local constraints that maintain a constant input to a given unit to global constraints that maintain the average connection strength of the entire network. In our work, we see how such constraints affect transitions to collective phenomena including synchronisation and collective chaos.
Constraints open up new ways to uncover the collective dynamics of adaptive networks. On the one hand, they allows us to develop and use mathematical techniques such as multiple timescale analysis to be applied in the context of adaptive networks. On the other hand, it opens up the question more generally as to what dependencies exist that manage the complexity of adaptivity in real world networks and what mechanisms realise them. In neural networks, for example, adaptivity of connection strengths is subject to metabolic constraints because of neurotransmitters involved. This may be a biological realisation of a constraint that influences the adaptation dynamics.
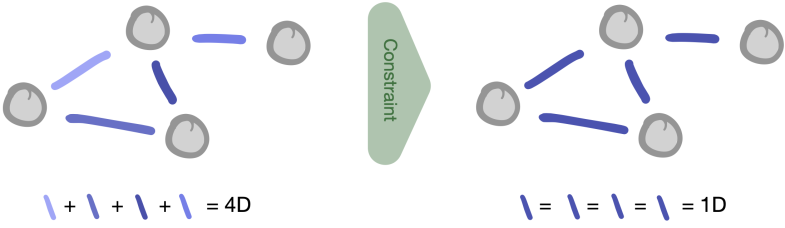
Figure: Adaptivity typically modulates weights associated with a connection. Four adaptive weights lead to four-dimensional adaptation dynamics (left). If the weights are constrained such that they are all the same (right) that reduces the dimension from four to one.
The paper Multiple timescale dynamics of network adaptation with constraints is published in Chaos with a separate summary in Scilight.
Christian Bick is Associate Professor at Vrije Universiteit Amsterdam and a Visiting Research Fellow in Oxford Mathematics.


