Galois Characterization of Henselian Fields
Abstract
I will talk about Jochen’s theorem about the existence of some non-trivial Henselian valuation given by investigating the absolute Galois group.
16:30
Torelli and Borel-Tits theorems via trichotomy
Abstract
Using the "trichotomy principle" by Boris Zilber I will give model theoretic proofs of appropriate versions of Torelli theorem and Borel-Tits theorem. The first one has interesting applications to anabelian geometry, I won't assume any prior knowledge in model theory.
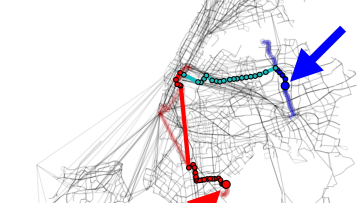
Many of us know the feeling of standing in front of a subway map in a strange city, baffled by the multi-coloured web staring back at us and seemingly unable to plot a route from point A to point B. Now, a team of physicists and mathematicians has attempted to quantify this confusion and find out whether there is a point at which navigating a route through a complex urban transport system exceeds our cognitive limits.
Extended QFT in Euclidean and Minkowskian signatures
Abstract
I'll explain the formalism of extended QFT, while
focusing on the cases of two dimensional conformal field theories,
and three dimensional topological field theories.
15:00
Computing Factor Tables, and Tables of Class Numbers
Abstract
Efficient factorization or efficient computation of class
numbers would both suffice to break RSA. However the talk lies more in
computational number theory rather than in cryptography proper. We will
address two questions: (1) How quickly can one construct a factor table
for the numbers up to x?, and (2) How quickly can one do the same for the
class numbers (of imaginary quadratic fields)? Somewhat surprisingly, the
approach we describe for the second problem is motivated by the classical
Hardy-Littlewood method.
Boundary Conditions, Mirror Symmetry and Symplectic Duality
Abstract
In the last few years, it has become clear that there are striking connections between supersymmetry and geometric representation theory. In this talk, I will discuss boundary conditions in three dimensional gauge theories with N = 4 supersymmetry. I will then outline a physical understanding of a remarkable conjecture in representation theory known as `symplectic duality.
15:00
Additive Combinatorics, Field Extensions, and Coding Theory.
Abstract
Additive combinatorics enable one to characterise subsets S of elements in a group such that S+S has small cardinality. In particular a theorem of Vosper says that subsets of integers modulo a prime p with minimal sumsets can only be arithmetic progressions, apart from some degenerate cases. We are interested in q-analogues of these results, namely characterising subspaces S in some algebras such that the linear span of its square S^2 has small dimension. Analogues of Vosper's theorem will imply that such spaces will have bases consisting of elements in geometric progression. We derive such analogues in extensions of finite fields, where bounds on codes in the space of quadratic forms play a crucial role. We also obtain that under appropriately formulated conditions, linear codes with small squares for the component-wise product can only be generalized Reed-Solomon codes. Based on joint works with Christine Bachoc and Oriol Serra, and with Diego Mirandola.
Tunneling in Theories with Many Fields
Abstract
The possibility of a landscape of metastable vacua raises the question of what fraction of vacua are truly long lived. Naively any would-be vacuum state has many nearby decay paths, and all possible decays must be suppressed. An interesting model of this phenomena consists of N scalars with a random potential of fourth order. We show that the scaling of the typical minimal bounce action with N is readily understood. We discuss the extension to more realistic landscape models as well as the effects of gravity.