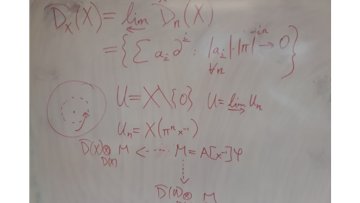11:00
Logic in practise
Abstract
In this talk we will introduce quantifier elimination and give various examples of theories with this property. We will see some very useful applications of quantifier elimination to algebra and geometry that will hopefully convince you how practical this property is to other areas of mathematics.