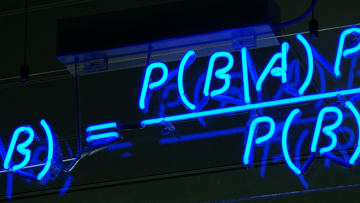TBA

We shall describe a new proof of the Mordell-Lang conjecture in positive characteristic, in the situation where the variety under scrutiny is a smooth subvariety of an abelian variety. 
Our proof is based on the theory of semistable sheaves in positive characteristic, in particular on  Langer's theorem that the Harder-Narasimhan filtration of sheaves becomes strongly semistable after a finite number of iterations of Frobenius pull-backs. Our proof produces a numerical upper-bound for the degree of the finite morphism from an isotrivial variety appearing in the statement of the Mordell-Lang conjecture. This upper-bound is given in terms of the Frobenius-stabilised slopes of the cotangent bundle of the variety.

I will describe some diophantine problems and results motivated by the analogy between powers of the modular curve and powers of the multiplicative group in the context of the Zilber-Pink conjecture.

The aim of this talk is to design an efficient multigrid method for constrained convex optimization problems arising from discretization  of  some  underlying  infinite  dimensional  problems. Due  to problem  dependency  of this approach, we only consider bound constraints with (possibly) a linear equality constraint. As our aim is to target large-scale problems, we want to avoid computation of second 
derivatives of the objective function, thus excluding Newton like methods. We propose a smoothing operator that only uses first-order information and study the computational efficiency of the resulting method. In the second part, we consider application of multigrid techniques to more general optimization problems, in particular, the topology design problem.

Partial differential equations with more than three coordinates arise naturally if the model features certain kinds of stochasticity. Typical examples are the Schroedinger, Fokker-Planck and Master equations in quantum mechanics or cell biology, as well as quantification of uncertainty.
The principal difficulty of a straightforward numerical solution of such equations is the `curse of dimensionality': the storage cost of the discrete solution grows exponentially with the number of coordinates (dimensions).

One way to reduce the complexity is the low-rank separation of variables. One can see all discrete data (such as the solution) as multi-index arrays, or tensors. These large tensors are never stored directly.
We approximate them by a sum of products of smaller factors, each carrying only one of the original variables. I will present one of the simplest but powerful of such representations, the Tensor Train (TT) decomposition. The TT decomposition generalizes the approximation of a given matrix by a low-rank matrix to the tensor case. It was found that many interesting models allow such approximations with a significant reduction of storage demands.

A workhorse approach to computations with the TT and other tensor product decompositions is the alternating optimization of factors. The simple realization is however prone to convergence issues.
I will show some of the recent improvements that are indispensable for really many dimensions, or solution of linear systems with non-symmetric or indefinite matrices.

Functions are usually approximated numerically in a basis, a non-redundant and complete set of functions that span a certain space. In this talk we highlight a number of benefits of using overcomplete sets, in particular using the more general notion of a "frame". The main 

benefit is that frames are easily constructed even for functions of several variables on domains with irregular shapes. On the other hand, allowing for possible linear depencies naturally leads to ill-conditioning of approximation algorithms. The ill-conditioning is 

potentially severe. We give some useful examples of frames and we first address the numerical stability of best approximations in a frame. Next, we briefly describe special point sets in which interpolation turns out to be stable. Finally, we review so-called Fourier extensions and an efficient algorithm to approximate functions with spectral accuracy on domains without structure.