Inversion in Volvox: Forces and Fluctuations of Cell Sheet Folding
Abstract
Tissue folding during animal development involves an intricate interplay
of cell shape changes, cell division, cell migration, cell
intercalation, and cell differentiation that obfuscates the underlying
mechanical principles. However, a simpler instance of tissue folding
arises in the green alga Volvox: its spherical embryos turn themselves
inside out at the close of their development. This inversion arises from
cell shape changes only.
In this talk, I will present a model of tissue folding in which these
cell shape changes appear as variations of the intrinsic stretches and
curvatures of an elastic shell. I will show how this model reproduces
Volvox inversion quantitatively, explains mechanically the arrest of
inversion observed in mutants, and reveals the spatio-temporal
regulation of different biological driving processes. I will close with
two examples illustrating the challenges of nonlinearity in tissue
folding: (i) constitutive nonlinearity leading to nonlocal elasticity in
the continuum limit of discrete cell sheet models; (ii) geometric
nonlinearity in large bending deformations of morphoelastic shells.
Coproducts in the cohomological DT theory of 3-Calabi-Yau completions
Abstract
14:00
Modeling and simulation of fluidic surfaces
Abstract
We briefly review mathematical models of viscous deformable interfaces (such as plasma membranes) leading to fluid equations posed on (evolving) 2D surfaces embedded in $R^3$. We further report on some recent advances in understanding and numerical simulation of the resulting fluid systems using an unfitted finite element method.
A link for this talk will be sent to our mailing list a day or two in advance. If you are not on the list and wish to be sent a link, please send email to @email.
14:00
Reconstructing Signals with Simple Fourier Transforms
Abstract
Reconstructing continuous signals based on a small number of discrete samples is a fundamental problem across science and engineering. In practice, we are often interested in signals with ``simple'' Fourier structure -- e.g., those involving frequencies within a bounded range, a small number of frequencies, or a few blocks of frequencies. More broadly, any prior knowledge about a signal's Fourier power spectrum can constrain its complexity. Intuitively, signals with more highly constrained Fourier structure require fewer samples to reconstruct.
We formalize this intuition by showing that, roughly speaking, a continuous signal from a given class can be approximately reconstructed using a number of samples equal to the statistical dimension of the allowed power spectrum of that class. We prove that, in nearly all settings, this natural measure tightly characterizes the sample complexity of signal reconstruction.
Surprisingly, we also show that, up to logarithmic factors, a universal non-uniform sampling strategy can achieve this optimal complexity for any class of signals. We present a simple, efficient, and general algorithm for recovering a signal from the samples taken. For bandlimited and sparse signals, our method matches the state-of-the-art. At the same time, it gives the first computationally and sample efficient solution to a broad range of problems, including multiband signal reconstruction and common kriging and Gaussian process regression tasks.
Our work is based on a novel connection between randomized linear algebra and the problem of reconstructing signals with constrained Fourier structure. We extend tools based on statistical leverage score sampling and column-based matrix reconstruction to the approximation of continuous linear operators that arise in the signal fitting problem. We believe that these extensions are of independent interest and serve as a foundation for tackling a broad range of continuous time problems using randomized methods.
This is joint work with Michael Kapralov, Cameron Musco, Christopher Musco, Ameya Velingker and Amir Zandieh
A link for this talk will be sent to our mailing list a day or two in advance. If you are not on the list and wish to be sent a link, please send email to @email.
14:15
Complex Links and Algebraic Multiplicities
Abstract
Given a nested pair X and Y of complex projective varieties, there is a single positive integer e which measures the singularity type of X inside Y. This is called the Hilbert-Samuel multiplicity of Y along X, and it appears in the formulations of several standard intersection-theoretic constructions including Segre classes, Euler obstructions, and various other multiplicities. The standard method for computing e requires knowledge of the equations which define X and Y, followed by a (super-exponential) Grobner basis computation. In this talk we will connect the HS multiplicity to complex links, which are fundamental invariants of (complex analytic) Whitney stratified spaces. Thanks to this connection, the enormous computational burden of extracting e from polynomial equations reduces to a simple exercise in clustering point clouds. In fact, one doesn't even need the polynomials which define X and Y: it suffices to work with dense point samples. This is joint work with Martin Helmer.
14:15
Application of a Bogomolov-Gieseker type inequality to counting invariants
Abstract
In this talk, I will work on a smooth projective threefold X which satisfies the Bogomolov-Gieseker conjecture of Bayer-Macrì-Toda, such as the projective space P^3 or the quintic threefold. I will show certain moduli spaces of 2-dimensional torsion sheaves on X are smooth bundles over Hilbert schemes of ideal sheaves of curves and points in X. When X is Calabi-Yau this gives a simple wall crossing formula expressing curve counts (and so ultimately Gromov-Witten invariants) in terms of counts of D4-D2-D0 branes. This is joint work with Richard Thomas.
The fluid mechanics of suspensions
Abstract
Materials made from a mixture of liquid and solid are, instinctively, very obviously complex. From dilatancy (the reason wet sand becomes dry when you step on it) to extreme shear-thinning (quicksand) or shear-thickening (cornflour oobleck) there is a wide range of behaviours to explain and predict. I'll discuss the seemingly simple case of solid spheres suspended in a Newtonian fluid matrix, which still has plenty of surprises up its sleeve.
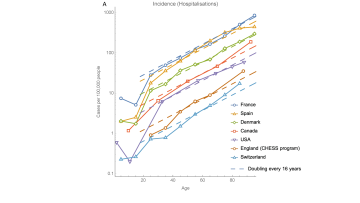
One of the great puzzles of the current COVID-19 crisis is the observation that older people have a much higher risk of becoming seriously ill. While it is usually commonly accepted that the immune system fails progressively with age, the actual mechanism leading to this effect was not fully understood. In a recent work, Sam Palmer from Oxford Mathematics and his colleagues in Cambridge have proposed a simple and elegant solution to this puzzle.