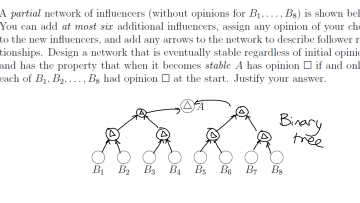
Brownian excursions, conformal loop ensembles and critical Liouville quantum gravity
Abstract
It was recently shown by Aidekon and Da Silva how to construct a growth fragmentation process from a planar Brownian excursion. I will explain how this same growth fragmentation process arises in another setting: when one decorates a certain “critical Liouville quantum gravity random surface” with a conformal loop ensemble of parameter 4. This talk is based on joint work with Juhan Aru, Nina Holden and Xin Sun.