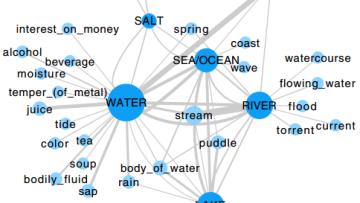
Semantics is the study of meaning as expressed through language, and it provides indirect access to an underlying level of conceptual structure. However, to what degree this conceptual structure is universal or is due to cultural histories, or to the environment inhabited by a speech community, is still controversial. Meaning is notoriously difficult to measure, let alone parameterise, for quantitative comparative studies.
Flowing to minimal surfaces
Abstract
For maps from surfaces there is a close connection between the area of the surface parametrised by the map and its Dirichlet energy and this translates also into a relation for the corresponding critical points. As such, when trying to find minimal surfaces, one route to take is to follow a suitable gradient flow of the Dirichlet energy. In this talk I will introduce such a flow which evolves both a map and a metric on the domain in a way that is designed to change the initial data into a minimal immersions and discuss some question concerning the existence of solutions and their asymptotic behaviour. This is joint work with Peter Topping.
Pee, Poo, and the Gut
Abstract
Fluids and solids leave our bodies everyday. How do animals do it, from mice to elephants? In this talk, I will show how the shape of urinary and digestive organs enable them to function, regardless of the size of the animal. Such ideas may teach us how to more efficiently transport materials. I will show how the pee-pee pipe enables animals to urinate in constant time, how slippery mucus is critical for defecation, and how the motion of the gut is related to the density of its contents, and in turn to the gut’s natural frequency.
More info is in the BBC news here: http://www.bbc.com/news/science-environment-34278595
11:00
"Definability of Derivations in the Reducts of Differentially Closed Fields".
Single Valued Elliptic Multizetas and String theory
Abstract
Modular invariance is ubiquitous in string theory. This is the symmetry of genus-one amplitudes, as well as the non-perturbative duality symmetry of type IIb superstring in ten dimensions. The alpha’ expansion of string theory amplitudes leads to interesting new modular forms. In this talk we will describe the properties of the new modular forms. We will explain that the modular forms entering the alpha’ expansion of genus one type-II superstring amplitude are naturally expressed as particular values of single valued elliptic multiple polylogarithm. They are natural modular generalization of the single valued elliptic multiple-zeta introduced by Francis Brown.
How a complex dynamic network such as the human brain gives rise to consciousness has yet to be established by science. A popular view among many neuroscientists is that, through a variety of learning paradigms, the brain builds relationships and in the context of these relationships a brain state acquires meaning in the form of the relational content of the corresponding experience.
The Manin-Mumford Conjecture via O-minimality
Abstract
In the talk I will give an introduction to the Manin-Mumford conjecture and to the Pila-Zannier strategy for attacking it in the case of products of elliptic curves. if the permits it, I will also speak about how this same strategy has allowed to attack the analogous André-Oort conjecture for Shimura Varieties of abelian type.
14:30
How accurate must solves be in interior point methods?
Abstract
At the heart of the interior point method in optimization is a linear system solve, but how accurate must this solve be? The behaviour of such methods is well-understood when a direct solver is used, but the scale of problems being tackled today means that users increasingly turn to iterative methods to approximate its solution. Current suggestions of the accuracy required can be seen to be too stringent, leading to inefficiency.
In this talk I will give conditions on the accuracy of the solution in order to guarantee the inexact interior point method converges at the same rate as if there was an exact solve. These conditions can be shown numerically to be tight, in that performance degrades rapidly if a weaker condition is used. Finally, I will describe how the norms that appear in these condition are related to the natural norms that are minimized in several popular Krylov subspace methods. This, in turn, could help in the development of new preconditioners in this important field.