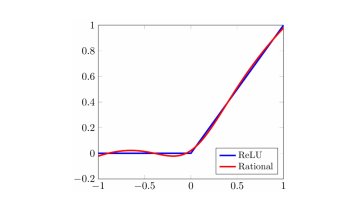
Deep learning has become an important topic across many domains of science due to its recent success in image recognition, speech recognition, and drug discovery. Deep learning techniques are based on neural networks, which contain a certain number of layers to perform several mathematical transformations on the input.
The Athena Swan Charter is a framework which is used across the globe to support and transform gender equality within higher education (HE) and research.
15:15
Factors in randomly perturbed graphs
Abstract
We study the model of randomly perturbed dense graphs, which is the union of any $n$-vertex graph $G_\alpha$ with minimum degree at least $\alpha n$ and the binomial random graph $G(n,p)$. In this talk, we shall examine the following central question in this area: to determine when $G_\alpha \cup G(n,p)$ contains $H$-factors, i.e. spanning subgraphs consisting of vertex disjoint copies of the graph $H$. We offer several new sharp and stability results.
This is joint work with Julia Böttcher, Olaf Parczyk, and Jozef Skokan.
Part of the Oxford Discrete Maths and Probability Seminar, held via Zoom. Please see the seminar website for details.
Singularities and the Einstein equations: Inextendibility results for Lorentzian manifolds
Abstract
Given a solution of the Einstein equations, a fundamental question is whether one can extend the solution or whether the solution is maximal. If the solution is inextendible in a certain regularity class due to the geometry becoming singular, a further question is whether the strength of the singularity is such that it terminates classical time-evolution. The latter question, as will be explained in the talk, is intimately tied to the strong cosmic censorship conjecture in general relativity which states in the language of partial differential equations that global uniqueness holds generically for the initial value problem for the Einstein equations. I will then focus in the talk on recent results showing the locally Lipschitz inextendibility of FLRW models with particle horizons and spherically symmetric weak null singularities. The latter in particular apply to the spherically symmetric spacetimes constructed by Luk and Oh, improving their C^2-formulation of strong cosmic censorship to a locally Lipschitz formulation.
Short polynomials in polynomial ideals
Abstract
How to calculate the minimal number of summands of a nonzero polynomial in a given polynomial ideal? In this talk, we first discuss the roots of this question in computational algebra. Afterwards, we switch to the viewpoint of a commutative algebraist. In particular, we see that classical tools from this field, such as primary decomposition or the Castelnuovo–Mumford regularity, fail to provide a solution to this problem. Finally, we discuss a concrete example: A standard determinantal ideal generated by $t$-minors does not contain any polynomials with fewer than $t!/2$ terms.