Vicky Neale and David Acheson are two of Oxford Mathematics's most engaging and accessible speakers and writers, and they both have new books to prove it.
The deformed Dixmier-Moeglin equivalence for completed enveloping algebras
Abstract
An algebra $R$ is said to satisfy the Dixmier-Moeglin equivalence if a prime ideal $P$ of $R$ is primitive if and only if it is rational, if and only if it is locally closed, and a commonly studied problem in non-commutative algebra is to classify rings satisfying this equivalence, e.g. $U(\mathfrak g)$ for a finite dimensional Lie algebra $\mathfrak g$. We explore methods of generalising this to a $p$-adic setting, where we need to weaken the statement. Specifically, if $\hat R$ is the $p$-adic completion of a $\mathbb Q_p$-algebra $R$, rather than approaching the Dixmier-Moeglin equivalence for $\hat R$ directly, we instead compare the classes of primitive, rational and locally closed prime ideals of $\hat R$ within suitable "deformations". The case we focus on is where $R=U(L)$ for a $\mathbb Z_p$-Lie algebra $L$, and the deformations have the form $\hat U(p^n L)$, and we aim to prove a version of the equivalence in the instance where $L$ is nilpotent.
Excursion Risk
Abstract
The risk and return profiles of a broad class of dynamic trading strategies, including pairs trading and other statistical arbitrage strategies, may be characterized in terms of excursions of the market price of a portfolio away from a reference level. We propose a mathematical framework for the risk analysis of such strategies, based on a description in terms of price excursions, first in a pathwise setting, without probabilistic assumptions, then in a Markovian setting.
We introduce the notion of δ-excursion, defined as a path which deviates by δ from a reference level before returning to this level. We show that every continuous path has a unique decomposition into δ-excursions, which is useful for scenario analysis of dynamic trading strategies, leading to simple expressions for the number of trades, realized profit, maximum loss and drawdown. As δ is decreased to zero, properties of this decomposition relate to the local time of the path. When the underlying asset follows a Markov process, we combine these results with Ito's excursion theory to obtain a tractable decomposition of the process as a concatenation of independent δ-excursions, whose distribution is described in terms of Ito's excursion measure. We provide analytical results for linear diffusions and give new examples of stochastic processes for flexible and tractable modeling of excursions. Finally, we describe a non-parametric scenario simulation method for generating paths whose excursion properties match those observed in empirical data.
Joint work with Anna Ananova and Rama Cont: https://ssrn.com/abstract=3723980
Elliptic stochastic quantisation and supersymmetry
Abstract
Stochastic quantisation is, broadly speaking, the use of a stochastic differential equation to construct a given probability distribution. Usually this refers to Markovian Langevin evolution with given invariant measure. However we will show that it is possible to construct other kind of equations (elliptic stochastic partial differential equations) whose solutions have prescribed marginals. This connection was discovered in the '80 by Parisi and Sourlas in the context of dimensional reduction of statistical field theories in random external fields. This purely probabilistic results has a proof which depends on a supersymmetric formulation of the problem, i.e. a formulation involving a non-commutative random field defined on a non-commutative space. This talk is based on joint work with S. Albeverio and F. C. de Vecchi.
Regularity and time discretization of extended mean-field control problems: a McKean-Vlasov FBSDE approach
Abstract
We analyze the regularity of solutions and discrete-time approximations of extended mean-field control (extended MFC) problems, which seek optimal control of McKean-Vlasov dynamics with coefficients involving mean-field interactions both on the state and actions, and where objectives are optimized over
open-loop strategies.
We show for a large class of extended MFC problems that the unique optimal open-loop control is 1/2-Hölder continuous in time. Based on the regularity of the solution, we prove that the value functions of such extended MFC problems can be approximated by those with piecewise constant controls and discrete-time state processes arising from Euler-Maruyama time stepping up to an order 1/2 error, which is optimal in our setting. Further, we show that any epsilon-optimal control of these discrete-time problems
converge to the optimal control of the original problems.
To establish the time regularity of optimal controls and the convergence of time discretizations, we extend the canonical path regularity results to general coupled
McKean-Vlasov forward-backward stochastic differential equations, which are of independent interest.
This is based on join work joint work with C. Reisinger and Y. Zhang.
16:00
North meets South colloquium
Abstract
Martin Gallauer (North): "Algebraic algebraic geometry"
If a space is described by algebraic equations, its algebraic invariants are endowed with additional structure. I will illustrate this with some simple examples, and speculate on the meaning of the title of my talk.
Zhaohe Dai (South): "Two-dimensional material bubbles"
Two-dimensional (2D) materials are a relatively new class of thin sheets consisting of a single layer of covalently bonded atoms and have shown a host of unique electronic properties. In 2D material electronic devices, however, bubbles often form spontaneously due to the trapping of air or ambient contaminants (such as water molecules and hydrocarbons) at sheet-substrate interfaces. Though they have been considered to be a nuisance, I will discuss that bubbles can be used to characterize 2D materials' bending rigidity after the pressure inside being well controlled. I will then focus on bubbles of relatively large deformations so that the elastic tension could drive the radial slippage of the sheet on its substrate. Finally, I will discuss that the consideration of such slippage is vital to characterize the sheet's stretching stiffness and gives new opportunities to understand the adhesive and frictional interactions between the sheet and various substrates that it contacts.
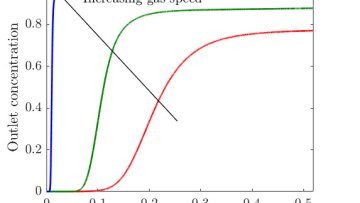
Oxford Mathematician Kristian Kiradjiev talks about his DPhil research, supervised by Chris Breward and Ian Griffiths in collaboration with W. L. Gore and Associates, Inc., on modelling filtration devices for removal of sulphur dioxide from flue gas.
12:00
Causal Relations At Infinity
Abstract
Motivated by an attempt to construct a theory of quantum gravity as a perturbation around some flat background, Penrose has shown that, despite being asymptotically flat, there is an inconsistency between the causal structure at infinity of Schwarzschild and Minkowski spacetimes. This suggests that such a perturbative approach cannot possibly work. However, the proof of this inconsistency is specific to 4 spacetime dimensions. In this talk I will discuss how this result extends to higher (and lower) dimensions. More generally, I will consider examples of how the causal structure of asymptotically flat spacetimes are affected by dimension and by the presence of mass (both positive and negative). I will then show how these ideas can be used to prove a higher dimensional extension of the positive mass theorem of Penrose, Sorkin and Woolgar.