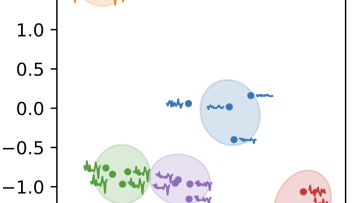
The square peg problem asks whether every Jordan curve in the
plane contains the vertices of a square. Inspired by Hugelmeyer's approach
for smooth curves, we give a topological proof for "locally 1-Lipschitz"
curves using 4-dimensional topology.

The second fundamental form of an embedded manifold must satisfy a set of constraint equations known as the Gauß-Codazzi equations. Since work of Chen-Slemrod-Wang, these equations are known to satisfy a particular div-curl structure: under suitable L^p bound on the second fundamental form, the curvatures are weakly continuous. In this talk we explore generalisations of this original result under weaker assumptions. We show how techniques from fluid dynamics can yield interesting insight into the weak continuity properties of isometric embeddings.

/

Teichmüller harmonic map flow is a geometric flow designed to evolve combinations of maps and metrics on a surface into minimal surfaces in a Riemannian manifold. I will introduce the flow and describe known existence results, and discuss recent joint work with M. Rupflin that demonstrates how singularities can develop in the metric component in finite time.

In this talk I will discuss some aspects of the potential theory, fine properties and boundary behaviour of the solutions to the Total Variation Flow. Instead of the classical Euclidean setting, we intend to work mostly in the general setting of metric measure spaces. During the past two decades, a theory of Sobolev functions and BV functions has been developed in this abstract setting.  A central motivation for developing such a theory has been the desire to unify the assumptions and methods employed in various specific spaces, such as weighted Euclidean spaces, Riemannian manifolds, Heisenberg groups, graphs, etc.

The total variation flow can be understood as a process diminishing the total variation using the gradient descent method.  This idea can be reformulated using parabolic minimizers, and it gives rise to a definition of variational solutions.  The advantages of the approach using a minimization formulation include much better convergence and stability properties.  This is a very essential advantage as the solutions naturally lie only in the space of BV functions. Our main goal is to give a necessary and sufficient condition for continuity at a given point for proper solutions to the total variation flow in metric spaces. This is joint work with Vito Buffa and Juha Kinnunen.

An 8-dimensional Riemannian manifold with holonomy group contained in Spin(7) is Ricci-flat, but not Kahler. The condition that the holonomy reduces to Spin(7) is equivalent to a complicated system of non-linear PDEs. In the non-compact setting, symmetries can be used to reduce this complexity. In the case of cohomogeneity one manifolds, i.e. where a generic orbit has codimension one, the non-linear PDE system
reduces to a nonlinear ODE system. I will discuss recent progress in the construction of 1-parameter families of complete cohomogeneity one Spin(7) holonomy metrics. All examples are asymptotically conical (AC) or asymptotically locally conical (ALC).

During this talk we will be interested in a one-dimensional exclusion process subject to strong kinetic constraints, which belongs to the class of cooperative kinetically constrained lattice gases. More precisely, its stochastic short range interaction exhibits a continuous phase transition to an absorbing state at a critical value of the particle density. We will see that the macroscopic behavior of this microscopic dynamics, under periodic boundary conditions and diffusive time scaling, is ruled by a non-linear PDE belonging to free boundary problems (or Stefan problems). One of the ingredients is to show that the system typically reaches an ergodic component in subdiffusive time.

Based on joint works with O. Blondel, C. Erignoux and M. Sasada

In practice, it is standard to initialize Artificial Neural Networks (ANN) with random parameters. We will see that this allows to describe, in the functional space, the limit of the evolution of (fully connected) ANN when their width tends towards infinity. Within this limit, an ANN is initially a Gaussian process and follows, during learning, a gradient descent convoluted by a kernel called the Neural Tangent Kernel. 

This description allows a better understanding of the convergence properties of neural networks, of how they generalize to examples during learning and has 

practical implications on the training of wide ANNs.