A is for Aperiodic Tiles
The Author

Professor Sir Roger Penrose FRS
Emeritus Rouse Ball Professor of Mathematics
Emeritus Fellow of Wadham College
Roger Penrose is a leading figure in cosmology and mathematical physics, and has won many accolades and prizes for his work, including the 1988 Wolf Prize for Physics, which he shared with Stephen Hawking. He has also written numerous books for a general audience, such as The Road to Reality and The Emperor's New Mind.
Find out more
This Eureka article also discusses aperiodic tiles and is written by Sir Roger Penrose.
Forbidden Crystal Symmetry was a lecture given by Sir Roger Penrose at the 2014 Alumni weekend on crystal and non-crystal symmetries.
A Knight on the tiles is an article by Plus Magazine in which Sir Roger Penrose discusses his ideas on Physics and Maths.
Extra Time: Professor Sir Roger Penrose in conversation with Andrew Hodges are two films exploring the development of Sir Roger Penrose's thoughts, ending with his most recent theories and predictions.

A is for Aperiodic Tiles
Outside the Andrew Wiles Building, the home of the Oxford Mathematical Institute, is a paved area.

As you can see, there are just two shapes of tile involved. What makes these tiles special is that the resulting tilings are necessarily non-periodic: it is not possible to create the tiling by taking some (potentially very large) section and repeating it over and over again. A set of tiles with this property is called aperiodic.
My investigations of aperiodic tiles did not start with these two shapes. I began by examining the subdivision of a regular pentagon into six smaller ones, leaving five small triangular gaps.

Having done this once, one can then apply the same process to each resulting pentagon, and then keep repeating in this way, at each stage scaling the pentagons up to their initial sizes.
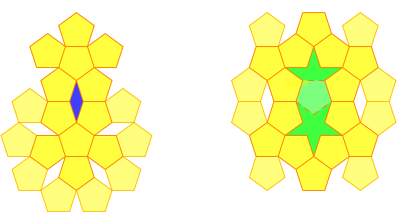
This gives us a very intriguing pattern which eventually led me to find a set of six tiles with the property that any tiling of the plane using them must arise from this iterative process, and is, moreover, consequently non-periodic.
Somewhat later, I learned that Raphael Robinson had, a few years earlier, also found an aperiodic set of six tiles, although his tiles were quite different from mine. However, I knew I could do better because, by making a small modification to my tiles, I could create an aperiodic set of just five tiles. Later, after a bit more cutting, pasting, and adapting, I found that just two tiles would suffice!
John Conway named my new tiles "kites" and "darts".
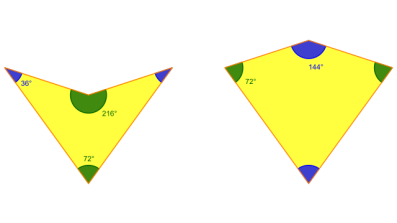
The colours of the vertices (corners) give matching rules: vertices of the same colour must be placed next to each other. This is to force the tilings to have the desired properties.

One nice property of the kites and darts is that they enable us to see directly that any tiling must be non-periodic, thanks to their scaling properties. Take a tiling using the kites and darts, such as the one above. Bisect each dart symmetrically with a straight cut. By recombining the half-darts and kites, we can make darts and kites on a larger scale which follow the same matching rules as before.

This "inflation" property proves the non-periodicity of any such tiling: if there were some region -- called a period parallelogram -- that could be repeated over and over again to yield the whole tiling, then this same region would have to be a period parallelogram for the inflated darts and kites too. By repeating this argument many times, we'd find that the inflated kites and darts would eventually be larger than the period parallelogram itself, which is not possible.
There are other ways of exploring the aperiodicity of these tile sets, such as via the ratio of kites to darts in regions of the tiling of ever increasing size. In the limit we get the golden ratio, a constant that occurs in many places in mathematics.
You might have noticed that the paving outside the Andrew Wiles Building doesn't use the darts and kites; instead it uses a pair of rhombuses. Again these have rules about matching vertices following a colouring as shown, and these rules force the resulting tilings to be non-periodic.
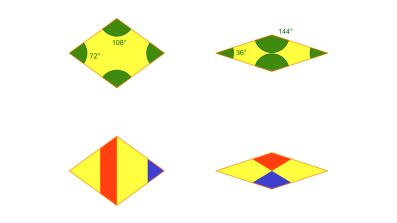
In fact, when I designed the paving for the Mathematical Institute I added an extra feature, the curved metal bands that link up to produce an overarching pattern. If you look carefully, you will see that there are still just two designs of tiles; these metal bands capture an intriguing aspect of the mathematical structure.
Whether there is an aperiodic set consisting of just a single shape, subject to such adjacency matching rules, is an unsolved problem...


