D is for Diophantine Equations
The Author

Dr Jonathan Pila FRS
Reader in Mathematical Logic
Jonathan Pila is a researcher working in model theory and number theory. He was awarded the Clay Research Award and the Senior Whitehead Prize by the London Mathematical Society in 2011. In particular, his research links structures in mathematical logic with Diophantine problems leading to exciting new applications and approaches.
Find out more
Nrich has a nice problem on Diophantine N-tuples.
Fermat's Last Theorem was the subject of a Horizon documentary, which is available on BBC iplayer.
The Clay Mathematics Institute Millenium Prize page on the unsolved conjecture of Birch and Swinnerton-Dyer gives a complete description of the problem.
Andrew Wiles was recently awarded the Abel Prize for solving Fermat's Last Theorem.
Triples and Quadruples is an article by Plus Magazine, linking Pythagoras to Fermat.
The book Fermat's Last Theorem by Simon Singh gives a history of the problem and sketches the journey of mathematical discovery to get to a proof.
D is for Diophantine Equations
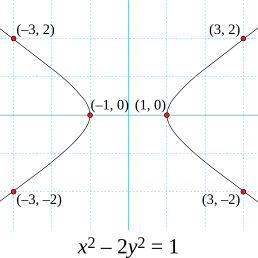
A diophantine equation is an algebraic equation, or system of equations, in several unknowns and with integer (or rational) coefficients, which one seeks to solve in integers (or rational numbers). The study of such equations goes back to antiquity. Their name derives from the mathematician Diophantus of Alexandria, who wrote a treatise on the subject, entitled Arithmetica.
The most famous example of a diophantine equation appears in Fermat’s Last Theorem. This is the statement, asserted by Fermat in 1637 without proof, that the diophantine equation $X^n + Y^n = Z^n$ has no solutions in whole numbers when $n$ is at least 3, other than the “trivial solutions” which arise when $XYZ = 0$. The study of this equation stimulated many developments in number theory. A proof of the theorem was finally given by Andrew Wiles in 1995.
The basic question one would like to answer is: does a given system of equations have solutions? And if it does have solutions, how can we find or describe them? While the Fermat equation has no (non-trivial) solutions, similar equations (for example $X^4 + 15Y^4 = Z^4$) do have non-trivial solutions. One of the problems on Hilbert’s famous list from 1900 was to give an algorithm to decide whether a given system of diophantine equations has a solution in whole numbers. In effect this is asking whether the solvability can be checked by a computer programme. Work of Martin Davis, Yuri Matiyasevich, Hilary Putnam and Julia Robinson, culminating in 1970, showed that there is no such algorithm. It is still unknown whether the corresponding problem for rational solutions is decidable, even for plane cubic curves. This last problem is connected with one of the Millennium Problems of the Clay Mathematics Institute (with a million dollar prize): the Birch—Swinnerton-Dyer Conjecture.
One could take the view that the existence of a finite number of solutions is merely accidental, and seek to decide whether a given system of equations has infinitely many solutions. For example, it is known that for any nonzero rational numbers $a$, $b$ and any $n >= 4$ the equation $ax^n + by^n = 1$ has only finitely many solutions. This is a special case of a 1983 result by Faltings affirming a 1922 conjecture by Mordell. One can give an upper bound on how many solutions there can be, but so far no-one has been able to bound how “complicated” the solutions might be (that is, to give an upper bound for their numerator and denominator), and so there is no known method to find all the solutions.
Euler conjectured a strengthening of Fermat’s Last Theorem: that if a sum of $n$ integers, each a $k$th power, is a $k$th power then $n \geqslant k$. For $n = 2$ this recovers Fermat’s Last Theorem. But the conjecture turns out to be wrong! A counterexample with $n = 4$ was found by Lander and Parkin in 1966: $27^5 + 84^5 + 110^5 + 133^5 = 144^5$, and counterexamples with $n = 3$ (and fourth powers) were found by Elkies in 1986.
Understanding the solutions of diophantine equations is certainly not easy. One can pose some more modest questions. For example, consider the equation $X^5 + Y^5 = Z^5 + T^5$ to be solved in positive integers $X, Y, Z, T$. It has infinitely many “obvious” solutions where $\{X, Y\} = \{Z, T\}$. It is believed, but not known, that these are the only solutions. Otherwise put, it is unknown whether there is an integer that can be written as a sum of two fifth powers in two different ways. But it has been shown (Erdős 1939, Hooley 1964) that, if one counts solutions up to a given large size, then the obvious solutions outnumber the non-obvious ones.
A wide variety of methods are employed to study diophantine equations. These include algebra, especially algebraic geometry, various analytic methods (using calculus), as well as methods from mathematical logic.
In fact, methods of all these types are currently used by people in the Oxford Mathematical Institute working on diophantine equations.