E is for Elliptic Curves
The Author

Dr Jennifer Balakrishnan
Titchmarsh Research Fellow and Junior Research Fellow at Balliol College
Jennifer Balakrishnan is a researcher working in number theory. She works on techniques to find rational points on curves and investigates invariants appearing in a $p$-adic version of the Birch and Swinnerton-Dyer conjecture.
Find out more
Plus Magazine has a great article on how elliptic curves are used in cryptography.
The Klein Project Blog links Heron's formula and elliptic curves.
Fermat's Last Theorem was the subject of a Horizon documentary, which is available on BBC iplayer.
Answers on a donut is an abridged version of Manjul Bhargava's Fields medal lecture, featuring hyperelliptic curves.
Download the A3 poster as a pdf
E is for Elliptic Curves
Appearing everywhere from state-of-the-art cryptosystems to the proof of Fermat's Last Theorem, elliptic curves play an important role in modern society and are the subject of much research in number theory today.
An elliptic curve $E$ defined over the rational numbers (fractions) is a smooth plane curve of the form
$$y^2 = x^3 + Ax + B$$
together with a special point $\mathcal{O}$ "at infinity".
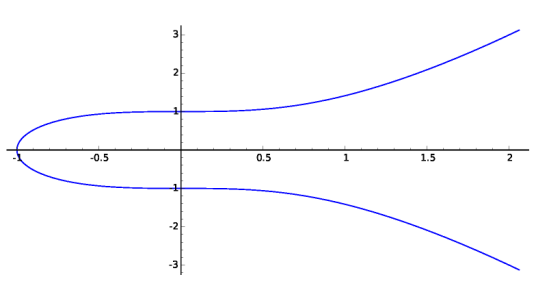
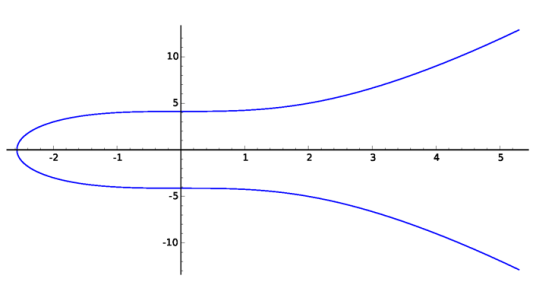
What do elliptic curves look like? We can plot elliptic curves in the real plane:
[above] The elliptic curve $E_1: y^2 = x^3 + 1$
[below] The elliptic curve $E_{17}: y^2 = x^3 + 17$
but actually these two graphs, while they look roughly the same, hide much of the interesting arithmetic structure of the two curves. To elaborate on this, let us consider the set of rational points $E(\mathbb{Q})$: the set of points $(x,y)$ with $x$ and $y$ both rational, satisfying the equation of $E$, together with the point $\mathcal{O}$.
A fundamental problem in the study of elliptic curves is the following: given an elliptic curve $E$ defined over the rationals, find its set $E(\mathbb{Q})$ of rational points. For example, the elliptic curve $E_1: y^2 = x^3 + 1$ has precisely 6 rational points, given by the set $\{\mathcal{O}, (-1,0), (0, \pm 1), (2, \pm 3) \}$. The elliptic curve $E_{17}: y^2 = x^3 + 17$ has, among its rational points, the following:
$$\mathcal{O}, (-1, \pm 4), (-2, \pm 3), (2, \pm 5), (4, \pm 9), \left(\frac{1}{4}, \pm \frac{33}{8}\right), (8, \pm 23), \left(-\frac{8}{9}, \pm \frac{109}{27}\right), \left(\frac{19}{25}, \pm \frac{522}{125}\right), \\(43, \pm 282), (52, \pm 375), \left(-\frac{64}{25}, \pm \frac{59}{125} \right), \left(\frac{94}{25}, \pm \frac{1047}{125}\right), ...$$
While $E_1$ has finitely many rational points, $E_{17}$ has infinitely many rational points - something that cannot be seen by looking at the real-valued graphs above.
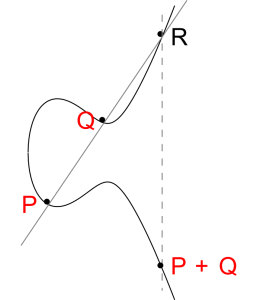
It turns out that the set $E(\mathbb{Q})$ of rational points enjoys additional structure: it is an abelian group. This means that given rational points $P$ and $Q$, there is a way to produce the sum $P+Q$, and this is another rational point. Indeed, there is a geometric way to carry out this addition. Draw the line through $P$ and $Q$. This intersects the elliptic curve in a third rational point $R$, and the reflection of $R$ in the $x$-axis is the sum $P+Q$, as seen here:
In 1922, Mordell proved that the set of rational points $E(\mathbb{Q})$ is a finitely generated abelian group. This means that any rational point $P$ can be written as a finite combination of certain generating points. For example, the points $P_1 = (-2, 3)$ and $P_2 = (-1, 4)$ are generators of the rational points of $E_{17}$. This means that all rational points on $E_{17}$ - even very complicated points - can be written in terms of these two points. For example, we have
$$ \begin{align} S & = \left(\frac{\small{\text{170914680007433755273838144758012}}}{\small{\text{111693884047097647373766735954481}}}, -\frac{\small{\text{5355483650472998648137959899973372475907238039375}}}{\small{\text{1180440469197546185983425190055773135812433974871}}}\right)\\ & = -5 P_1 + 5 P_2. \end{align}$$
One difficult open question is the following: given an elliptic curve $E$ over the rationals, how do we find the generators of $E(\mathbb{Q})$? In fact, giving an algorithm to calculate how many (independent infinite-order) generators there are - a quantity known as the algebraic rank of $E(\mathbb{Q})$ - would be a breakthrough. This is the subject of the Birch and Swinnerton-Dyer conjecture, one of the Clay Mathematics Institute's million-dollar Millennium Prize Problems. The conjecture is that the algebraic rank of $E(\mathbb{Q})$ is equal to another invariant associated to $E$, its analytic rank, the order of vanishing of an object known as the $L$-function $L(E,s)$ attached to $E$ at the point $s = 1$.
The elliptic curve $L$-function plays a very important role in modern number theory. Perhaps the most celebrated theorem of our era is the fact that elliptic curves over the rationals are modular: that is, the $L$-function of an elliptic curve defined over the rationals is equal to the $L$-function of a cusp form. In 1994, Wiles and Taylor-Wiles proved this result for semistable elliptic curves over the rationals and, in so doing, proved Fermat's Last Theorem. This correspondence between elliptic curves and cusp forms - through the theory of Galois representations - now motivates an exciting area of research known as the Langlands problem.