F is for Fourier Transform

Aled Walker

Postgraduate student 

Aled Walker is an analytic number theorist in the second year of his DPhil, under the supervision of Prof. Ben J. Green, studying a bouquet of topics which find themselves at the intersection of number theory, combinatorics, and analysis. He is currently working on a project studying systems of simultaneous diophantine inequalities in the primes, attempting to apply the recent advances of Green-Tao and Green-Tao-Ziegler on linear equations in primes.

The Fourier Transform is used in a wide range of disciplines and activities - it can even save your life! Find out how in Plus Magazine's two articles on the mathematics of tomography (the second article discusses the mathematics behind tomography).

For the musically inclined you can find out how the Fourier transform can lead to a career in audio software engineering. 

Underground Mathematics has some activities for school students interested in finding out more about the Fourier Transform.

For a short history of the Fourier Transform see this Guardian article.

If you're confused about what the Fourier Transform actually is - Stack Overflow has the answer.

Terence Tao has also written a good introductory paper on the Fourier Transform.

The Fourier Transform can be applied to many things:

One of the reasons it's so powerful is that it breaks down any periodic function into a combination of sines and cosines. You can also do this for orbits with Ptolemy's system of epicycles and deferents:

Download the A3 poster as a pdf
 

The Fourier transform is that rarest of things: a mathematical method from over 200 years ago which not only remains an active area of research in its own right, but is also an invaluable tool in nearly every branch of mathematics. Though originally developed by Fourier in 1807 to help solve certain partial differential equations, the transform is a living example of a remarkable feature of mathematics, that a tool created in one sub-discipline can break through these artificial classifications and become vital in another. I am particularly interested in applications of the Fourier transform to problems in Combinatorics and Number Theory.

School students learn that one can express points in three-dimensional space $\mathbb{R}^3$ by three standard coordinates. The first-year undergraduate then learns that there are different sets of coordinates for the same point, depending on the basis for $\mathbb{R}^3$ which is chosen, and that a different basis could be better suited to the particular problem at hand. When the vector space is not $\mathbb{R}^3$ but rather a space of functions $f:G\longrightarrow \mathbb{C}$ for a (locally compact abelian) group $G$ -- the reals $\mathbb{R}$, the integers $\mathbb{Z}$, the unit circle $\mathbb{R}/\mathbb{Z}$, or the finite cyclic group $\mathbb{Z}/N\mathbb{Z}$, say -- a particularly useful 'basis' is supplied by so-called characters on $G$. In the case of $\mathbb{R}$, these are continuous functions of the form $x\mapsto e^{2 \pi i k x }$, for some fixed $k\in\mathbb{R}$. The 'coordinate' of a function $f$ with respect to a phase $e^{2 \pi i k x }$ is recorded by its Fourier transform $\widehat{f}:\mathbb{R}\longrightarrow \mathbb{C}$, defined as $$\widehat{f}(k) = \int\limits_{-\infty}^{\infty}f(x)e^{-2\pi i k x  } \, dx.$$ Provided that $f$ is suitably 'nice' -- a smooth function with quickly decaying derivatives, for example -- one may recover $f$ from its Fourier transform, via the inversion formula $$f(x) = \int\limits_{-\infty}^{\infty}\widehat{f}(k)e^{2\pi i k x  } \, dk.$$ An analogous inversion formula holds for functions on $\mathbb{Z}$, namely
\begin{align*}
\widehat{f}(\alpha) &= \sum\limits_{n\in \mathbb{Z}} f(n)e^{-2\pi i \alpha n}\\
f(N)& = \int\limits_{0}^{1} \widehat{f}(\alpha)e^{2\pi i \alpha N } \, d\alpha.
\end{align*}

Our mentioning of functions on $\mathbb{Z}$ heralds the connection with Number Theory. It is an old result of Lagrange, from 1770, that every positive integer $N$ can be written as the sum of four squares, but a rather more difficult task is to provide a good estimate for the number of different such representations. Early in the 20th century the British mathematicians Hardy and Littlewood found the key.

The argument runs more simply when considering sums of five squares. Let $r(N)$ be the representation function, so $r(N)$ counts the number of ways to write $N$ as a sum of five squares.

By Fourier inversion, $$r(N) = \int\limits_{0}^{1} \widehat{r}(\alpha)e^{2\pi i \alpha N} \, d\alpha = \int\limits_{0}^{1} S(\alpha)^5 e^{2\pi i \alpha N} \, d\alpha,$$ where $$S(\alpha) = \sum\limits_{n\leqslant N^{\frac{1}{2}}} e^{-2\pi i \alpha n^2}.$$

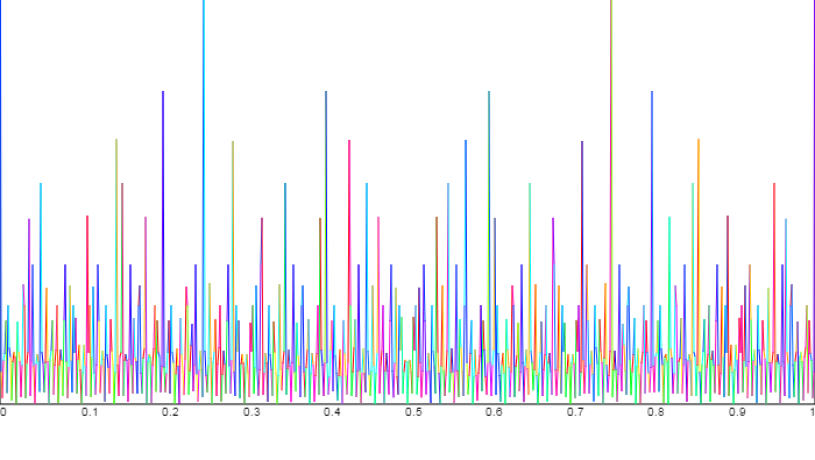
Estimating the size of $r(N)$ is equivalent to estimating this integral. It turns out that $S(\alpha)$ is largest when $\alpha$ is 'close' to a rational number with small denominator, and in this case $S(\alpha)$ and the contribution to the integral may be explicitly calculated. These $\alpha$ are called the 'major arcs'. For all other $\alpha$, called the 'minor arcs', a device known as Weyl's inequality may be used to show that $S(\alpha)$ is small, and hence the integral over the minor arcs only contributes to the error in our estimate for $r(N)$. A graph for $N=600$, with $\alpha$ on the $x$-axis and $\vert S(\alpha)\vert$ on the $y$-axis, is shown below.

Graph by Eugen Keil showing the peaks near rational numbers.

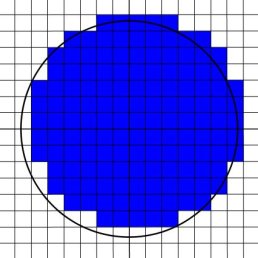
We have tapped a rich vein.  The 'Gauss circle problem' asks us to find the number of integer lattice points inside a circle: for a fixed large $r$, we want to determine the number of integers $m$, $n$ such that $m^2 + n^2 \leq r^2$. A fundamental property of the Fourier transform called Poisson summation, which states that $$\sum\limits_{n\in \mathbb{Z}}f(n) = \sum\limits_{k\in \mathbb{Z}}\widehat{f}(k),$$ refines the error term in this problem.

The fact that a set of integers with a large Fourier coefficient enjoys concentration on an arithmetic progression allowed Klaus Roth, in 1953, to prove that if $N$ is large enough, then any subset of the integers $\{0,1,\cdots,N-1\}$ of size at least $\frac{N}{1000}$ contains three equally spaced points.

And finally, the generality of the modern theory was used to great effect by John Tate, in his famous PhD thesis of 1950, helping to provide a deep proof of one of the most beautiful relationships in mathematics -- the analytic class number formula. This equation demonstrates the relationship between factorisation in a quadratic number field and the value $L(1,\chi)$ of a Dirichlet $L$-function, and Tate's proof used generalised Poisson summation on a certain locally compact abelian group called the adeles. We may conjecture that Fourier himself would have been very surprised indeed to see his method for understanding heat-flow used for such remarkable ends!