M is for Morphogenesis

Dr Thomas Woolley

Senior Lecturer, University of Cardiff [previously postdoctoral researcher, University of Oxford]

Thomas Woolley specialises in mathematical biology, where his doctorate focused on understanding the pattern formation behind fish spots and zebra stripes. Alongside this research he now investigates mathematical models of stem cell movement. The hope is that by understanding how stem cells move we can influence them and thus speed up the healing process. He is experienced in mathematical outreach activities. Most recently he was the Fellow of Modern Mathematics at the London Science Museum and helped redesign their mathematics gallery.

Dr Andrew Krause

Departmental Lecturer in Applied Mathematics

Andrew Krause is an applied mathematician working in mathematical biology and nonlinear dynamical systems. A large focus of his work is on understanding complex extensions of classical reaction-diffusion models which might be more physically and biologically relevant to understand pattern formation in nature. Besides pattern formation, he has worked on a number of other projects, from modelling invasions in ecology and cancer, to studying the chaotic rotation of celestial bodies and cell growth in tissue engineering bioreactors.

Thomas Woolley gave a TEDx talk on Mighty Morphogenesis in 2015.

Plus Magazine has an article on How the Leopard Got Its Spots.

The Turing Pattern Project is a collaborative national project to engage primary school children with nature and mathematics.

Forging patterns and making waves from biology to geology: a commentary on Turing (1952) ‘The chemical basis of morphogenesis’ by Philip Ball gives more background and information.

More on Alan Turing and animal patterns (video with James Grime and Thomas Woolley). 

Download the A3 poster as a PDF

How did the leopard get its spots? 

How did the zebra get its stripes? 

Outside of Rudyard Kipling’s Just So Stories, mathematics might just hold the answers. One theory behind nature’s beautiful patterns (known as morphogenesis, meaning “creation of form”) stems from a highly counter-intuitive idea concocted in 1952 by the tragic genius that was Alan Turing. 

Turing’s theory depends on a couple of factors. Firstly, we need two interacting populations called morphogens. Today, we usually think of these as being proteins, or other biological entities. Critically, although the morphogens are able to enhance and inhibit each other’s production and degradation, Turing assumed that the reactions were “stable”, which simply means that the morphogens would settle into a fixed state if well-mixed. 

The second component of Turing’s theory assumes that the morphogens are able to diffuse around their spatial domain. Diffusion is the random motion of particles as they bounce off one another. It is the process behind smells spreading out through the air and ink spreading out through water. In both these scenarios, and more generally, diffusion acts to wipe out non-uniformity. Thus, over time, diffusion tends to homogenize everything - the opposite of forming patterns. 

As you can see, neither of Turing’s ingredients produce patterns alone. Moreover, one might think that they would actively work against pattern formation. However, this is where Turing’s genius shines through. He noticed that if you chose the right stable biochemical interactions and allowed them to diffuse at different rates, then patterns could not only be sustained, but appear spontaneously. 

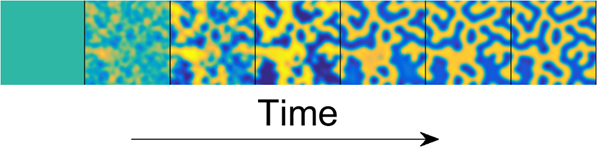
Turing’s theory of morphogenesis is incredibly powerful, as it offers a whole range of different patterns. The labyrinthine patterns seen above, as well as the spots and stripes seen in the animations below, all arise from the same model, under small adjustments to the parameter values. Thus we can find the whole of nature inside this mathematical framework. 

These simulations are examples of these ideas on curved surfaces (mathematically, a 2-manifold) to demonstrate how changes in curvature can affect the resulting patterns. Combinations of Turing's ideas with other kinds of instabilities lead to the second and third examples, which show not just spatial pattern formation, but patterns which continuously evolve in space and time. The final example demonstrates something called 'spatiotemporal chaos,' which is an active area of research.

Of course, animals do not need to be told how to produce patterns; their skin pigments develop naturally. So, what is the use of this theory? Beyond allowing us to understand the evolutionary constraints of skin patterns these ideas have the potential to explain mechanisms underlying human development. For example, you start out as a highly homogeneous spherical egg, yet once the egg is fertilised you develop into your highly heterogeneous body, with arms, legs, fingers and toes. 

We aren’t there yet, but as Turing once said: 

“We can only see a short distance ahead, but we can see plenty there that needs to be done.” 

References 

Diffusion image attained from Wikipedia and used under the creative commons license. https://en.wikipedia.org/wiki/Diffusion#/media/File:Blausen_0315_Diffus…;

Animations copyright Andrew Krause

Pattern emergence image copyright Thomas E. Woolley 

Cover image obtained from Nature, credit Getty Images