Episode 11

In episode 11, Ittihad shows us a variety of cute olympiad-style problems!
Further Reading
The Monk Problem - Intermediate Value Theorem
In the solution to the monk problem we talked about the idea that if one monk is going up the mountain, and one monk is coming down the mountain, then they must cross somewhere in between.
You’ve met something like this already if you’ve seen the “change of sign method” – suppose $f$ is a function with $f(a)>0$ and $f(b)<0$. Then somewhere in between $a$ and $b$ there is a value $c$ say with $f(c)=0$... provided that $f$ is a continuous function, although you probably weren’t told that last part at A-level or equivalent (in fact, you might have only seen this stated as a true fact about polynomials at A-level).
Both of these problems; the monks passing each other, and the change of sign method, are consequences of the Intermediate Value Theorem; roughly speaking, this says that a continuous function going from one value to another must go through every intermediate value somewhere in between. Here’s a Khan Academy video that introduces the Intermediate Value Theorem, if you’d like to see a technical statement of the theorem.
Geometry problem
Here’s the geometry question that we put on screen at the end of the livestream. You’ll need to find a good angle of attack for this one.
In quadrilateral WXYZ, with perpendicular diagonals, we are given angles $\angle WZX = 30^\circ$, $\angle XWY = 40^\circ$, and $\angle WYZ = 50^\circ$. What is the value of angle $\angle ZXY$?
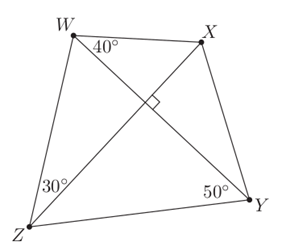
If you can do this problem, here’s a harder version; write $\alpha$ for angle $\angle WZX$, write $\beta$ for angle $\angle XWY$, and write $\gamma$ for angle $\angle WYZ$. Can you find angle $\angle ZXY$ in terms of $\alpha$, $\beta$, and $\gamma$?
One more problem
We didn’t have time for this problem in the livestream. Some of you might have seen it before since it’s a bit of a classic problem, but for the people seeing this problem for the first time; it’s a classic for a reason- it’s a great problem!
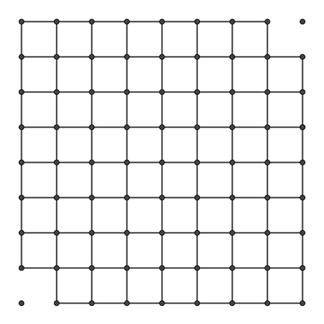
You’re given a square grid made of 8 by 8 small squares, but with two opposite corner squares removed. You’re also given a collection of 31 dominos- each domino is a 2 by 1 rectangle that can exactly covers two adjacent squares. Can you cover all of the 62 squares with the dominoes?
Other problem solving questions
Ittihad likes the book “Problem-Solving Strategies” by Arthur Engel as a source of interesting Olympiad-like Mathematics problems. That book seems to be quite expensive though, if you want to legally own a physical copy of the book; I think it might be out of print.
You might also be interested in this collection of past British Maths Olympiad questions; https://bmos.ukmt.org.uk/home/bmo.shtml.
Curve Sketching
$$y=\sin^2x,\quad y=\sin^4 x, \quad y=\sin^6 x,\quad\dots$$
Sketch the first two on the same axes, being careful near the points where $y=0$ and the points where $y=1$. Think about how your sketch would change for $y=\sin^6 x$ and so on, with higher and higher even powers.
If you want to get in touch with us about any of the mathematics in the video or the further reading, feel free to email us on oomc [at] maths.ox.ac.uk.

