Episode 4

In episode 4, all the problems involve pigeons. James is joined by current student Christian to explain.
Further Reading
Pigeonhole principle
Here’s a clear statement of the pigeonhole principle;
“If there are $m$ pigeons in $n$ pigeonholes, with $m\geq kn+1$, then at least one pigeonhole contains at least $k+1$ pigeons”.
The homework problem that we didn’t answer on the livestream is as follows;
“If nine points are placed in a square of side length 2, prove that there are three of them which form a triangle of area ½ or less, or find an example where this isn’t the case”.
Group Theory
On the livestream, I couldn’t spell the word “associativity” which might have stopped you from looking it up. It’s a property that a “binary operation” might have. A binary operation is something that takes two inputs and gives one output (like adding numbers together, or finding the average of two numbers, or raising the first number to the power of the second number). Some of these satisfy $x*(y*z)=(x*y)*z$, where $*$ is a sort of placeholder symbol to represent your binary operation (you could imagine putting a + there, for example).
Associativity is one of the four properties that you need to satisfy in order for your binary operation and set together to be a “group”, https://mathworld.wolfram.com/Group.html.
Quickest Routes
We talked on the livestream about a clever reflection trick. As a result of that, the angle between the river and the incoming path is the same as the angle between the river and the outgoing path. That’s how reflecting a laser beam works too.
I briefly mentioned a different problem that derives Snell’s Law. This one needs a bit of calculus, so ignore it for now if you haven’t seen the chain rule yet.
Suppose you’re on a beach with a straight boundary between the sand and the sea. If you want to get from a point on the beach to a point in the sea, then you need to run on the sand a bit, and then swim in the sea a bit. We’re going to think about where you should get into the sea.
Suppose you’re 10m away from the sand/sea boundary, and you see someone in trouble at a fixed point 10m out to sea, and 20m down the shoreline. You can run at speed 10 m/s, and you can swim at speed 2 m/s. You plan to do something like this (not a straight line because you want to exploit your superior running speed).
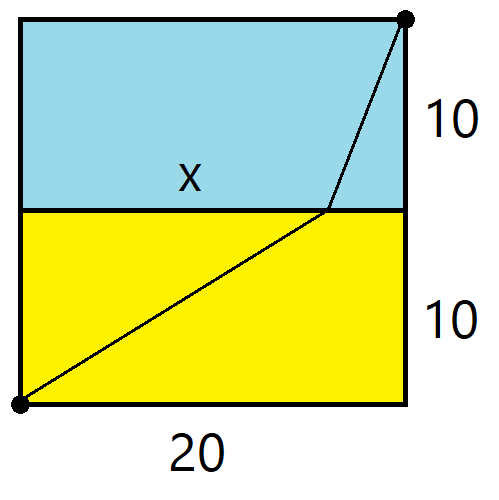
Use geometry to work out how long it takes you to get to the person in trouble, in terms of $x$, the distance along the beach where you get into the sea. Use calculus to find an equation that the distance $x$ satisfies when this function is minimised. Interpret this equation in terms of angles at the point where you get in the sea. Compare with Snell’s Law https://en.wikipedia.org/wiki/Snell%27s_law.
If you find this sort of thing interesting, then you might like this Feynman lecture; https://www.feynmanlectures.caltech.edu/II_19.html.
That suggests two methods for the sand/sea problem; one where you do the calculus, and one method where you quote Snell’s Law. I am not aware of any equivalent to the clever reflection trick for the sand/sea problem!
If you want to get in touch with us about any of the mathematics in the video or the further reading, feel free to email us on oomc [at] maths.ox.ac.uk.

