Episode 5

In episode 5, Deepak presents Fantastic Graphs and Where to Find Them. We also revisit a pigeonhole principle question from episode 4.

Further Reading

Homework problems

Sketch these two separate curves;

$$\text{(a)} \quad y=x^2e^{-x^2} \qquad \text{(b)} \quad y=\frac{e^x}{e^x+1}.$$

One of these functions is related to the Maxwell-Boltzmann distribution for the random speeds of gas particles at a particular temperature, and one of them is used in some neural nets to switch on or off each neuron in response to an input signal.

Elliptic curves

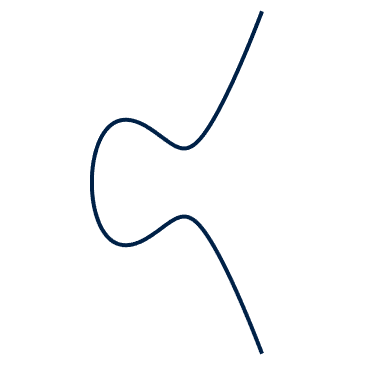
We sketched the curve $y^2=x^3-2x+2$ on the livestream. Here’s a summary of a process that you could use for sketching curves like this (without using any differentiation)

• Sketch the cubic on the right hand side
• We want $y=\pm\sqrt{\text{this cubic}}$ so we need to look at the cubic we’ve sketched and imagine the square root of the value at each value of $x$. Something funny is going on though- if the cubic is negative then there isn’t a real square root, so there are no corresponding values of $y$. So our curve only exists for particular values of $x$ where that cubic is positive.
• Sketch a distorted version of the cubic in regions where it’s positive
• Add in the reflection in the $x$-axis.

If you want to get the turning points in the right places, or work out what’s going on near points on the $x$-axis, then you’ll need to know a bit of differentiation. On the livestream, Deepak used implicit differentiation to work out the gradient of the curve (the slope of the tangent line at any given point). It’s not super-important how this calculation works, but let’s look at the answer. If you haven't seen implicit differentiation, you can join in with this next bit by just taking it as read that this is a formula for how steep the gradient of a tangent to the curve is at any point. The gradient is $$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{3x^2-2}{2y}.$$

So when we get close to the $x$-axis, $y$ gets really small, and this expression gets really large. That’s why this elliptic curve goes vertical as it crosses the $x$-axis.

Here’s a Desmos workbook where you can explore what happens when you change the coefficients; https://www.desmos.com/calculator/vxx8nvhv6y

Sometimes the elliptic curve is connected, and sometimes it’s in two separate parts. This is related to the number of roots that the cubic on the right-hand side has.

There are some special cases when the cubic on the right has a repeated root. In that case, something different happens when the curve meets the $x$-axis. Can you set the sliders in the Desmos workbook to find this special case? What can you see where the curve meets the $x$-axis? For those who know about implicit differentiation: what’s the derivative near this point? Why does the argument above about the gradient being infinite not hold here?

Astroids

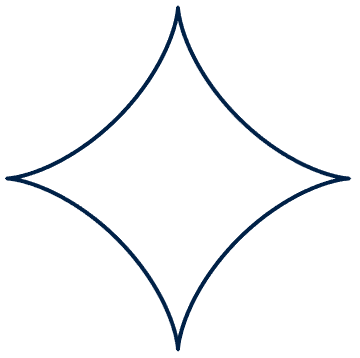
One way to construct this shape is to roll a circle of radius 1 around a circle of radius 4 and track the position of one point on the small circle (there’s a toy like this where you put a pencil through a hole in the small circle and trace out the shape). There’s a nice animation at https://mathworld.wolfram.com/Astroid.html. Guess how many times the small circle rotates as it goes around the large circle. Watch the animation carefully. Were you correct?

In general, if the large circle is $R$ times bigger than the smaller circle, you can make other shapes. What condition is needed on the number $R$ for the point on the small circle to get back to where it started after one trip around the big circle? What condition is needed on $R$ for the point to eventually come back to where it started (perhaps after multiple trips around the big circle)? What condition is needed on the number $R$ for the point opposite the starting point to be on the curve?

These shapes are called Hypocycloids, and you can see some more animations at https://mathworld.wolfram.com/Hypocycloid.html

If you’ve learned about parametric equations, you can plot these in Desmos!

There’s a related, but slightly simpler problem related to a circle rolling on flat ground. This gives a shape called a cycloid https://mathworld.wolfram.com/Cycloid.html. And that reminds me of a different problem; if you have square wheels, what shape should you make the road in order to keep your axle at a constant ride-height? There’s an animation of how this works on Wikipedia here; https://commons.wikimedia.org/wiki/File:Rolling-Square_colored.gif and people have even built working models- see http://stanwagon.com/!

If you want to get in touch with us about any of the mathematics in the video or the further reading, feel free to email us on oomc [at] maths.ox.ac.uk.