Episode 7

In episode 7, James describes the chain rule for differentiation, including a higher-dimensional version.
Further Reading
Summing consecutive integers
The new additions to last week’s problem are
- Can you make all the numbers that aren’t powers of 2?
- How many ways are there to write a given number as a sum of consecutive integers?
If you like this sort of problem (adding integers together), then you might be interested in the following problem;
Which numbers can be written as the sum of two prime numbers?
This is the Goldbach conjecture, and it’s unsolved. Here’s a link to a Numberphile video about it and a link to a relevant xkcd.
Partial Derivatives
On the livestream, we talked very briefly about the partial derivatives $\displaystyle \frac{\partial f}{\partial x}$ and $\displaystyle \frac{\partial f}{\partial y}$. I thought I could use the further reading to show you an example of how you might calculate these in practice. This is possibly the most technical thing I've ever put in the further reading, so it's a bit of an experiment. Skip this if you would rather be reading about ellipses or curve sketching.
Suppose we have $f(x,y)=x^4-4x^2+xy$. If we wanted to plot this, we might sketch some sort of 3D picture with $z=f(x,y)$.
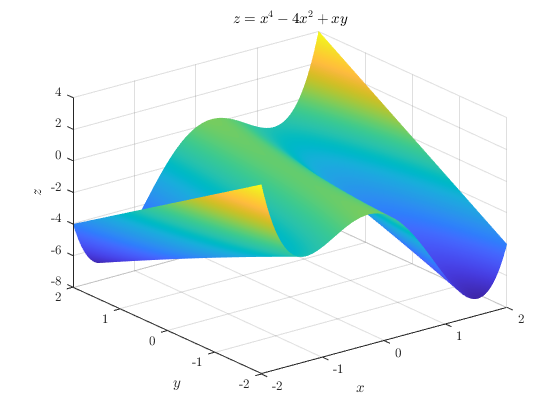
The idea for $\displaystyle \frac{\partial f}{\partial x}$ is that we want to find the derivative with respect to $x$ while we keep $y$ constant. We could imagine taking a slice through that 3D picture with $y$ constant.
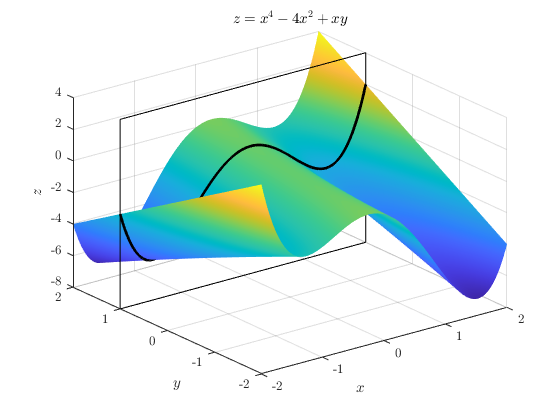
With $y$ constant, we can happily differentiate each term with respect to $x$. The first two terms give us $4x^3-8x^2$ in the normal way. When we get to the $xy$ term, well $y$ is constant, so this is just $(\text{constant}\times x)$. We know how to differentiate that with respect to $x$ too! It's just $(\text{constant})$. Here the constant is $y$, but that's OK because we're treating $y$ as a constant for this derivative. Putting it together, our partial derivative is
$$
\frac{\partial f}{\partial x}=4x^3-8x+y
$$
This depends on $x$ and $y$. It describes the way that the function increases if you were to start a point on the surface and then move a little bit in the $x$-direction.
We can also work out the partial derivative with respect to $y$.
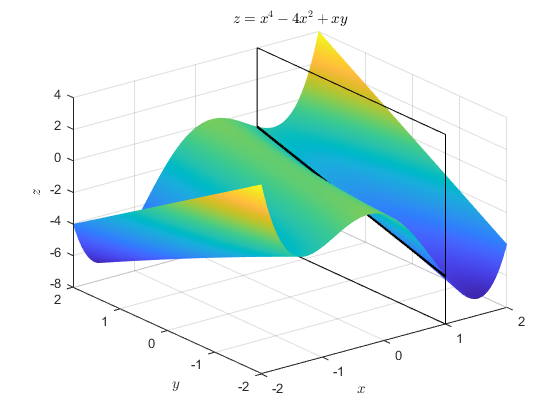
From this point of view, $x$ is a constant, so the first two terms $x^4-4x^2$ are just a constant, and so the partial derivative with respect to $y$ of those terms is just zero. The last remaining term gives us
$$
\frac{\partial f}{\partial y}=x
$$
Together, these partial derivatives can be used for lots of things, like working out the tangent plane to the surface, approximating the function, or finding the normal to the surface. It’s also used in gradient descent in machine learning. Wikipedia has a surprisingly narrative analogy for gradient descent. I’m not aware of many analogies on Wikipedia, so this one is worth reading here.
Ellipse stretching and squashing
Let’s have another go at that “stretch and squash” method for finding tangents to an ellipse.
Suppose we’ve got the ellipse $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$ and we want to find the tangent at a point $(x,y)$. Let’s consider the transformation $u=x/a$ and $v=y/b$, which is a sort of squashing in the $x$-direction and the $y$-direction. Over here, $u^2+v^2=1$ is a circle. Since tangents to a curve stay tangent when you squash coordinates, all we need to do is find the tangent to the circle and stretch back to our original coordinates. OK, we’re at the point $(u,v)=(x/a,y/b)$, and the gradient of the radius of this circle is $v/u$. Since the tangent to a circle is at right angles to the radius, the gradient of the tangent is $-u/v=-xb/ya$. Now when we stretch back, the gradient is going to be affected by the stretching (the tangent stays tangent, but the actual value of the gradient changes when we do the stretch). The stretch parallel to the $y$-direction increases the gradient by a factor of $b$, and the stretch parallel to the $x$-direction decreases the gradient by a factor of $a$. So transforming back to the original problem, the gradient here is $-xb^2/ya^2$.
It’s interesting to think about what stays the same and what changes when you stretch the coordinate axes. Areas change in a predictable way, and the ratios between areas stay the same. Angles don’t stay the same. The lengths of line segments don’t stay the same (or even stay in the same ratio). That's why the equation for the perimeter of an ellipse is so complicated; it's $4aE\left(\sqrt{1-\frac{b^2}{a^2}}\right)$ where $E(x)$ is the complete elliptic integral of the second kind, which you might learn about in a course on integral transforms at university one day.
Curve Sketching
Unrelated to everything in this episode, here are two more curves that you could try sketching
$$\text{(a)}\quad \sin\left(e^{-x}\right), \qquad \text{(b)} \quad e^{-1/x^2} $$
One of these is an interesting function that I saw in an Analysis lecture, and the other is an idealised glissando.
If you want to get in touch with us about any of the mathematics in the video or the further reading, feel free to email us on oomc [at] maths.ox.ac.uk.

