Season 2 Episode 5

In this episode, James explores a geometry problem with a complicated answer, and discovers an ancient formula along the way. There's also an arithmetic problem, and a geometry puzzle based on a band logo.
Further Reading
Overlapping circles
On the livestream we calculated the area of overlap of two circles with radii $r_1$ and $r_2$ when their centres are separated by distance $d$. I think that the final answer is something like $$\phi r_1^2 - \frac{r_1^2\sin 2\phi}{2}+\theta r_2^2 - \frac{r_2^2\sin 2\theta}{2}$$
where
$$\theta=\cos^{-1}\left(\frac{r_2^2+d^2-r_1^2}{2r_2d}\right)\quad\text{and}\quad \phi=\cos^{-1}\left(\frac{r_1^2+d^2-r_2^2}{2dr_1}\right)$$
I’m using radians for the angles here. Phew! If the circles have the same radius, then this simplifies quite a bit (partly because $\theta=\phi$ in that case).
There’s an interesting case where the area inside both circles is exactly half of the area of each circle (so that the three regions formed are all the same size). That happens if $r_1=r_2$ and if $$2 \theta -\sin 2\theta = \frac{\pi}{2}\quad \text{where}\quad\theta=\cos^{-1} \left(\frac{d}{2r}\right)$$
I couldn't see a nice way to solve that equation exactly, so I solved it numerically (using Newton-Raphson from A-level Maths, in case anyone’s interested) to find $\theta\approx 1.155$ and so $d=2r\cos\theta\approx 0.8079$. This allows me to draw the “perfect Venn diagram” where all the areas are equal.
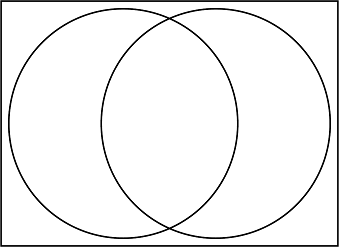
I’ve added a rectangle around the outside, chosen carefully so that the area outside both circles but inside the rectangle matches the area inside both circles. I had a spare parameter to play with, so I made the minimum gap between the circles and the rectangle at the top and bottom the same as the minimum gap on the sides. Here's a slightly tedious exercise to try at home; work out the side lengths of the rectangle in terms of $r$ and $d$ so that all the conditions above are satisfied. I had to do it to draw the picture!
MAT question with horses
Here’s the MAT question that I showed you part of. Please note that this question was written in terms of radians. MAT questions from 2018 onwards are written in terms of degrees. If the function $\cos^{-1}$ returns angles measured in degrees, then the “area that neither can reach” in (iii) would be $\frac{1}{45^\circ}\cos^{-1}\left(\frac{\sqrt{\pi}}{2}\right)-\sqrt{\frac{4-\pi}{\pi}}$.
MAT 2017 Q4
A horse is attached by a rope to the corner of a square field of side length 1.
(i) What length of rope allows the horse to reach precisely half the area of the field?
Another horse is placed in the field, attached to the corner diagonally opposite from the first horse. Each horse has a length of rope such that each can reach half the field.
(ii) Explain why the area that both can reach is the same as the area neither can reach.
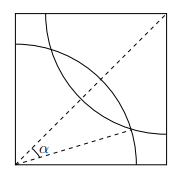
(iii) The angle $\alpha$ is marked in the diagram above. Show that $\alpha = \cos^{-1}\left(\frac{\sqrt{\pi}}{2}\right)$ and hence show that the area neither can reach is $ \frac{4}{\pi}\cos^{-1}\left(\frac{\sqrt{\pi}}{2}\right) - \sqrt{\frac{4 - \pi}{\pi}}$. Note that $\cos^{-1}$ is also known as $\arccos$.
A third horse is placed in the field, and the horses are rearranged. One horse is now attached to the midpoint of the bottom side of the field, an
(iii) Given each horse can access an equal area of the field and that none of the areas overlap, what length of rope must each horse have to minimise the area that no horse can reach?
The horses on the bottom and left midpoints of the field are each replaced by goats; each goat is attached by a rope of length $g$ to the same midpoint as in part (iii). The remaining horse is attached to the upper right corner with rope length $h$.
(iv) Given that $0 \leqslant h \leqslant 1$, and that none of the animals' areas can overlap, show that $\frac{\sqrt{5}- 2}{2} \leqslant g \leqslant \frac{1}{2\sqrt{2}}$ holds if the area that the animals can reach is maximised.
The solution for this MAT question is available here (pdf).
Curve sketching
$$y=x-\sin(x)\quad\text{with $x$ measured in radians}$$
This is related to the overlapping circles question above.
$$y=x-2\sin(x)\quad\text{with $x$ measured in radians}$$
This one is a little bit different.
See also; MAT 2016 Q1E here (pdf).
If you want to get in touch with us about any of the mathematics in the video or the further reading, feel free to email us on oomc [at] maths.ox.ac.uk.

