Season 2 Episode 6
Have you ever thought about what might happen if we tried to combine complex numbers and integration? In this episode, we explore what that might involve! There's a surprising link between integration, complex numbers, and logarithms.
Further Reading
Contour Integration
The livestream was an attempt to introduce the idea of “contour integration” to you. I’m not sure that I did a great job of explaining what that actually involves, so here’s some further reading to find out more about how $\int_\gamma f(z) \,\mathrm{d}z$ might be defined for integration along a curve or “contour” called $\gamma$.
First, we should try to understand a line integral (sometimes, rather charmingly, called a “curtain integral”). The idea here is that, if our function takes 2D coordinates as input, then we can choose a path in those coordinates and integrate along that path, adding up small contributions from the value of the function along the path, just like we do when imagining normal integration. There is a really good animation on Wikipedia for this. The rest of that Wikipedia page is a bit too complicated for us today (I think it says “tensor” too much to be helpful right now), but look at the section headings briefly – this article covers vectors, flow fields, complex numbers, and quantum mechanics!
That idea of an integral “along a line” is important for complex integration, because it helps us to understand how to deal with complex numbers as the input to the function (imagining complex numbers as being just like $(x,y)$-coordinates in the normal way; with their real and imaginary parts as the coordinates – this is called the “Argand diagram” interpretation of complex numbers).
For contour integration of a function $f(z)$ we need one more abstraction – the functions that we’re interested in today have complex output as well as complex input. So the values we get “along the curve” are complex numbers. That’s a little bit tricky to visualise, and I have to admit that normally I make no attempt to visualise it while working with contour integration. Slight tangent here; just visualising the function is tricky, before we do any integrals. People sometimes plot the imaginary and real parts separately with a colour scale or as a surface (where the height, the “z” variable, represents either the real or the imaginary part). See this page for some examples of what I mean.
With both of those ideas (complex input, and complex output), we’ve just about got an idea of what $\int_\gamma f(z)\,\mathrm{d}z$ might mean. In the livestream, we then tried it out, using my computer to add together contributions along the contour.
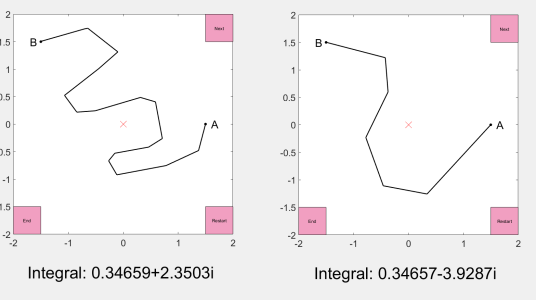
First, we tried $f(z)=1/z$ and $\int_\gamma f(z)\,\mathrm{d}z$ with $\gamma$ going from A to B via the bit of the $(x,y)$-plane with $y>0$. It didn’t seem to matter what route the path $\gamma$ took, we always got the same answer for the integral. We could even make the path more complicated and go into the half of the plane with $y<0$ and we were fine, until we tried a path around the “other side” of the origin. The integral was different, by a factor of about $2\pi i$. This was a bit surprising!
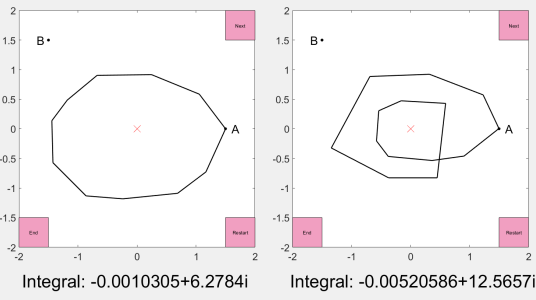
To investigate further, we looked at a new path that loops from A to A (you could imagine this as the combination of a path away from A, followed by the reverse of a different path away from A. That might sound like a strange thing to imagine, but it highlights the idea that we’re looking at the difference between two different paths away from A, which is how we discovered this in the previous experiment). We found that if we integrate around the origin in a clockwise direction, we get $-2\pi i$, and if we integrate around the origin in an anticlockwise direction, we get $2\pi i$. If we loop twice around the origin in an anticlockwise direction, we get $4\pi i$.
This is part of an amazing result called Cauchy’s Residue Theorem; for a differentiable complex function $f(z)$,
$$\oint_\gamma f(z)\,\mathrm{d}z = 2\pi i \sum_{k} I(\gamma,a_k)\operatorname{Res}(f,a_k).$$
This says that the integral around a closed curve $\gamma$ just depends on behaviour of the function at any “poles” at points $a_k$ inside the curve. There are two things inside the sum there; the first $I(\gamma,a_l)$ is called the “winding number” and it’s just a count of how many times the contour $\gamma$ goes around the point $a_k$. The winding number doesn’t depend on the function, and it’s easy to work out. In practice you’d work this out by looking at your curve and counting how many times it goes around $a_k$ (it’s usually just "one" in practice, if your curve doesn’t cross itself). The other thing $\operatorname{Res}(f,a_k)$ is called the “residue” of the function at $a_k$ and it doesn’t depend on $\gamma$. Essentially, you find the bit of your function that looks like $\frac{A}{x-a_k}$ and the residue is just the coefficient $A$. If your function is complicated then you might need to do some sort of Taylor-series-like expansion near $a_k$ to work out what that coefficient is, which can be a little bit fiddly. But it doesn’t involve $\gamma$ at all, so that’s great!
To put this in context, it's a bit like if I claimed that whenever you integrate a real polynomial from $a$ to $b$, the answer is just the constant term of the polynomial, independent of $a$ and $b$, and independent of all the other coefficients in the polynomial. That’s obviously nonsense! But something similar to that level of nonsense is true for differentiable complex functions, integrated around closed curves.
For more on the Residue Theorem, see Wikipedia (quite technical, but has some examples of using this to do maths) or Mathworld (focus on a particular calculation which explains the formula above, including the factor of $2\pi i$).
I’d like to wrap up this section by saying that integration still works in the same sort of way as normal real functions – so for example if $\gamma$ is a path from $a$ to $b$ then $\int_\gamma 3z^2+iz\,\mathrm{d}z=\left[z^3+iz^2/2\right]_a^b=\left(b^3+ib^2/2\right)- \left(a^3+ia^2/2\right)$. For functions without any poles (points with explosive behaviour like $1/x$), everything is fine.
Curve sketching
It’s a bit of an open-ended challenge this week – I’d like to encourage you to try and visualise the complex function given by $f(z)=1/z$. That’s taking an input $x+iy$ and giving output $(x-iy)/(x^2+y^2)$. Maybe you could try to sketch the real and imaginary parts, or maybe you’ve got another idea for how we should imagine this.
If you want to get in touch with us about any of the mathematics in the video or the further reading, feel free to email us on oomc [at] maths.ox.ac.uk.

