Season 5 Episode 9

Truchet tiles are small patterned tiles that create larger patterns when they're arranged together with random orientations. Mochan is on the livestream in this episode to explore how many patterns we can form.
Further Reading
Desmos plots
I just had to get Desmos to have a go at Truchet tiles; Desmos | Truchet is my implementation of quarter-circle Truchet tiles. Hit the shuffle button to re-roll all the random orientations of the tiles. If your computer is struggling, reduce $N$.
Long-time fans of the show with a very good memory will know that I particularly like this one pattern which minimises the total length needed to connect the four corners of a square.
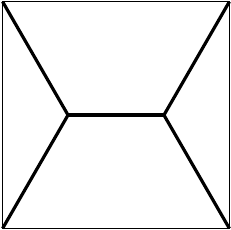
It’s the answer to a problem to do with minimising road network lengths, it’s what soap films do in some situations, and it can be drawn on the faces of a cube to make a diagram of a dodecahedron.
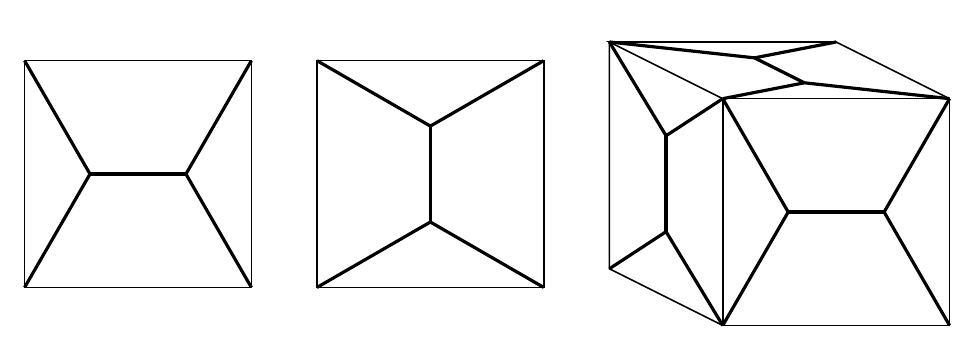
It’s also a way of decorating a square that has two orientations. So I set up Desmos to do a sort of Truchet-style tessellation with it.
Desmos | Roads and Truchet and Pentagons
This makes a random mix of pentagons, hexagons, and rhombuses, which is more than I expected.
Chalkdust articles
This livestream uses images from two really good Chalkdust articles; Too good to be Truchet by Colin Beveridge and When Truchet met Chladni by Stephen Muirhead.
Chalkdust is a free online magazine for the mathematically curious. It’s got some serious articles, and some… less serious articles.
Computer Generation
If you can make a computer write forward-slash and back-slash characters (that's / and \) at random then we can make a sort of Truchet tiling grid. The BASIC code for this is
10 PRINT CHR$(205.5+RND(1)); : GOTO 10
which is the name of a book by MIT professor Nick Montfort et al.
Percolation
Suppose you’re at an airport and they’ve got those queue barriers up; there’s a grid of posts, and two neighbouring posts are either connected with a barrier (with probability $p$) or they’re not. You’d like to know whether you can get through the maze of barriers or not. It depends a bit on the probability $p$ of course, and also on the network structure of the posts (square grid, or triangular grid, or something different). But in most cases there tends to be a sharp transition from "no you probably can't" to "yes you probably can". This happens at a probability known as the "percolation threshold" which depends on the grid
This is an active area of research. There’s some industrial interest in this sort of problem, because some people would like to get fossil fuels like oil out of the ground more efficiently.
Elsewhere in Mathematics, there’s a related idea in the theory of random graphs; if you join vertices at random, sometimes you get a massive connected component.
Generative art
See this blog post for some ideas about how to use Truchet Tiles in generative art. That example uses "winged" Truchet tiles which extend beyond the square and overlap; they look a lot more complicated than the Truchet tiles on the livestream, but the idea is the same. See this webpage for more.
If you want to get in touch with us about any of the mathematics in the video or the further reading, feel free to email us on oomc [at] maths.ox.ac.uk

