Season 6 Episode 2

On this episode, we're revisiting a classic livestream on the sums of two squares.

Sums of two squares

The thing that we proved with the product of two sums of two squares was known in the third century AD, more than a thousand years before mathematicians started exploring complex numbers. So the first vaguely unsatisfying proof is at least a thousand years older than the “better” proof. Perhaps we can speculate about things that currently seem really complicated but which might, in a thousand years, have a nice proof.

Once you’re done exploring and experimenting with this problem, you might like to look at the answer Sum of two squares theorem. But where's the fun in that?

Fans of extending this to more squares might like Legendre's three-square theorem and Lagrange's four-square theorem (why isn't there a five-square theorem?) The sum of three cubes problem is unsolved at time of writing; recent progress was to write the number 42 as the sum of three cubes (that link goes to a Numberphile video which is part of this playlist; progress has been made in the time since Numberphile started making videos)

Twenty-six

Is 26 the only number which is one more than a square and one less than a cube? I mentioned in passing that I thought this was an open problem. I don’t know why I thought that; I can’t find any reference online to that being the case. In fact, the only reference I can find is this this paper (cited by Wikipedia on the page for the number 26).

This proof uses complex numbers and rings and I haven’t understood it yet. It’s way out of the scope of what you’ll do at A-level or equivalent. If I can get my head around this and work out how to explain it in terms of A-level maths, then it might turn into a future episode.

Seeing the Wikipedia page for the number 26 has reminded me of the following logic puzzle; what is the smallest positive whole number that doesn't have a Wikipedia page? That would be pretty notable; perhaps notable enough for us to make a Wikipedia page about that number, listing this as one of its properties? Oh no.

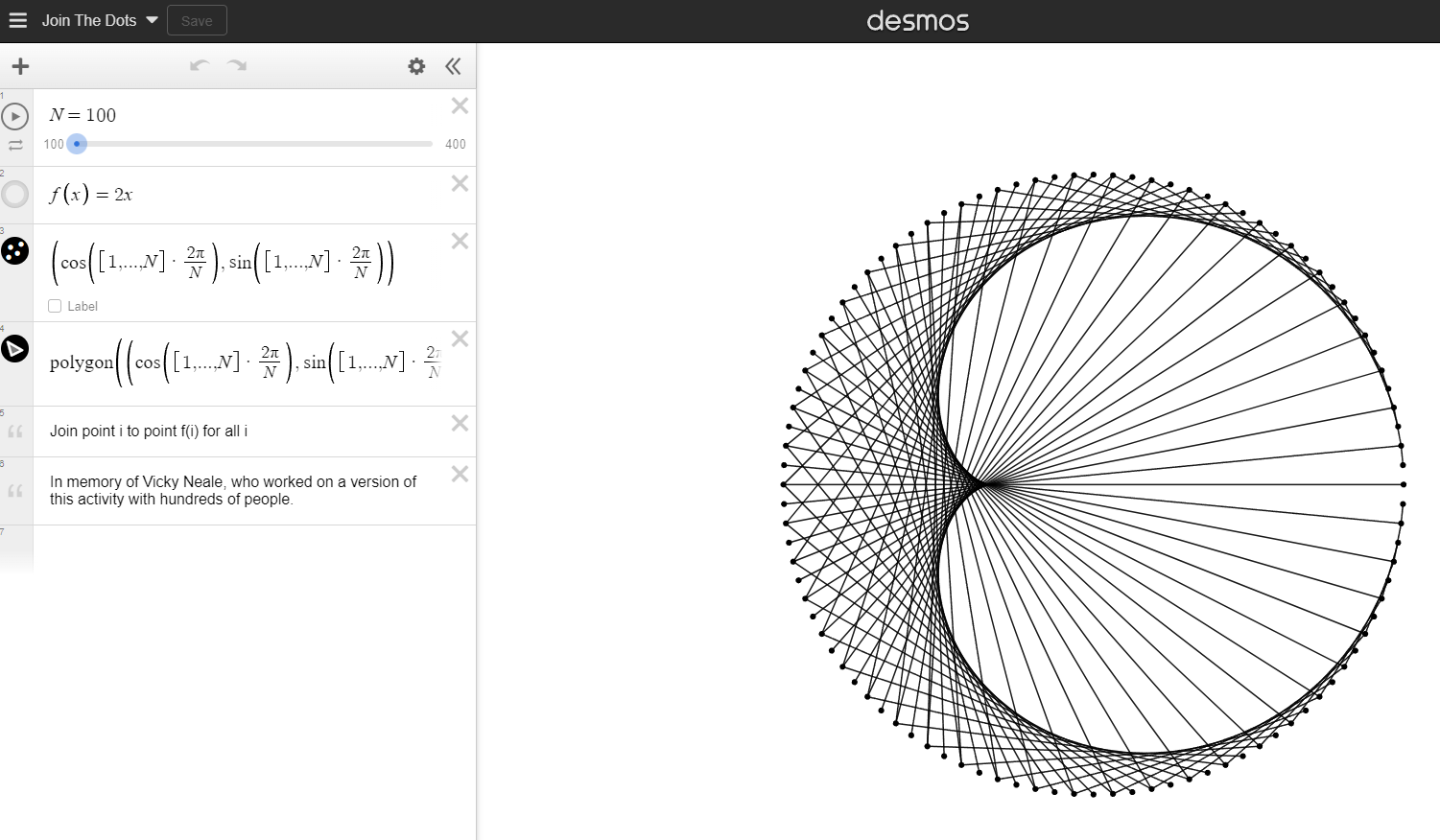
Join The Dots

Here’s a Desmos version of the last activity we tried, where you can change the number of points and change the rule for how points are joined;

Screenshot of a Desmos activity showing a circle of dots, with each one connected to its double. The lines are all tangent to a heart-shaped curve inside the circle.

Curves

On the livestream we saw something that looked like a heart and something that looked like a kidney; a cardioid.

We also saw a kidney-shaped nephroid.

A nephroid - a closed curve with two lobes or separate bumps. Something like a kidney bean, perhaps.

More generally, you might like Epicycloids. Also of interest are Hypotrochoids. Mostly I like these Wikipedia pages for the animations.

An epicycloid - a closed curve with more lobes. It's roughly like a flower sort of shape, with small lobes around the outside of a roughly circular shape.

I think I mentioned the Spirograph on the livestream, but I've realised that perhaps it was a bit of a 90s thing. Here's a link for anyone who hadn't heard of this toy.

Four-colouring

Someone in chat suggested colouring this in with four colours (it’s a reference to the four-colour map theorem). In fact, you can colour all of these patterns that come out of that Desmos activity with fewer than four colours. Can you see why?

Vicky Neale

Here are some cool things Vicky Neale made or did;

The book Closing the Gap on recent progress to understand gaps between prime numbers
The book Why Study Mathematics? about maths at university
A stitched version of the join-the-dots activity we did on the livestream
Prime scarves
Still the best introduction to induction in my opinion, even though she wrote it ages ago as a PhD student, before she went on to do all this other cool stuff
A brilliant open day talk on primes, number theory, elliptic curves, and more. We used to run this twice a day over the open days and people would come back to see it again in the same day, it's that good. The YouTube recording has almost half a million views.

Repeating patterns and doubling

This livestream repeated a topic from before. Pleasingly, it was previously Season 3 Episode 1 and now it's Season 6 Episode 2. So the topic is, itself, connected to its double.

If you want to get in touch with us about any of the mathematics in the video or the further reading, feel free to email us on oomc [at] maths.ox.ac.uk.