Season 7 Episode 10

Partitions

A partition of an integer $n$ is a set of positive integers ${a_1,a_2,a_3,\dots , a_k}$ such that $a_1\geq a_2 \geq a_3 \geq \dots \geq a_k$ and $a_1+a_2+a_3+\dots+a_k=n$.

For example, we might try to find all the partitions of $4$. These are ${1,1,1,1}$, ${2,1,1}$, ${2,2}$, ${3,1}$, ${4}$. Note that ${1,3}$ is not a partition of $4$, because it doesn’t obey the inequality condition. Note that ${3,2}$ is not a partition of $4$, because it doesn’t obey the "sum to 4" condition. For completeness, note that ${2,3}$ is not a partition of $4$, because it doesn’t obey either condition.

Whenever you meet a new definition, it’s a good idea to work out some examples and some non-examples for yourself, and I’d encourage you to do that now, with a different value of $n$.

We can represent these partitions in “Young diagrams”.

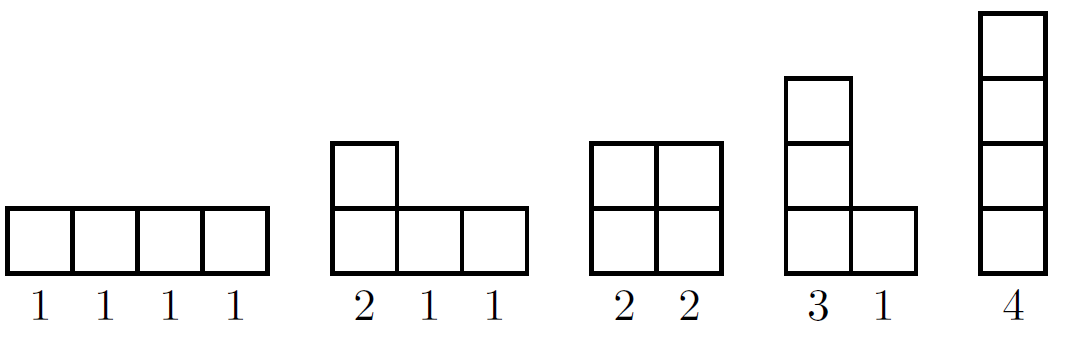
You might like to draw Young diagrams for partitions of $n$ with the value of $n$ you chose above.

Here’s a fact about partitions.

Claim: The number of partitions of $n$ into $k$ parts is the same as the number of partitions of $n$ into parts where the largest part is $k$. 

Before we see the proof, check that this is true for $n=4$ using the partitions above, and check that it’s true for your value of $n$ too. 

Proof: Consider the Young diagrams for the partitions of $n$. We need to find a pairing between each partition into $k$ parts and each partition with largest part $k$. 

We can make such a pairing by reflecting the diagrams in a diagonal line (it would be the line $y=x$ if the diagram were drawn onto the $(x,y)$-plane in the obvious way). 

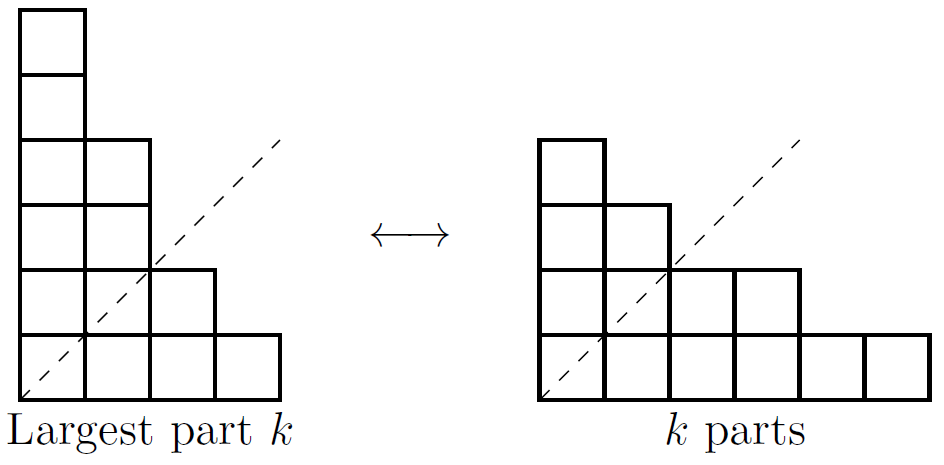
Each pairing with $k$ parts is paired with its mirror image, which has largest part $k$. □

Something distracting about the problem above is that some partitions both have $k$ parts and have largest part $k$; they’re in both sets! This doesn’t actually affect the argument above; some such partitions will be paired with themselves, some won’t, but it doesn’t matter; we’re not obliged to pair each such partition with itself.

This reflected image is called the conjugation of a partition. Can you find some examples of partitions that don’t change under conjugation? Can you find an example of a partition with 4 parts and with largest part 4 and which does change under conjugation? Make sure that your partitions obey the inequality condition in the definition.

Here are some more examples of things that you can prove about partitions. These have been left as exercises for you.

1. The number of partitions of $n$ into distinct, odd, parts, is the same as the number of partitions that don’t change under conjugation.
2. (Harder) The number of partitions of $n$ into odd parts is the same as the number of partitions of $n$ into distinct parts.
3. (Harder) The number of partitions of $n$ is the coefficient of $x^n$ in $$\prod_{i\geq 1} \frac{1}{1-x^i}$$

That last question includes an example of something called a generating function. See, for example, these notes from MIT for more.

If you want to get in touch with us about any of the mathematics in the video or the further reading, feel free to email us on oomc [at] maths.ox.ac.uk.