Season 7 Episode 7

Kempe chains and the Five Colour Map Theorem

The $n$-colour map theorem can be thought of as a graph theory problem, thinking of the countries as vertices of the graph, connected with an edge if they share a border. One of the nice things about graph theory is that you don't need to know much other maths to get stuck in, so I can link you to the Oxford course notes here.

Those lecture notes contain a proof of the five-colour theorem using induction on the size of the graph (page 21). The key idea is to consider a vertex with five or more neighbours that you haven’t coloured yet. If the neighbours only use four colours, you can pick the remaining colour for this vertex and you’re done. Otherwise, investigate whether you can flip the colour of one of the neighbours of a vertex (so that you have a colour free to colour this last vertex), or whether that flip would induce a chain of consequences that comes back to bite you by flipping the colour of another neighbour of your uncoloured vertex. The proof is that there’s always such a chain, for planar maps.

The topology of the map matters in the following sense; draw a little plus sign + on your map. Can you draw a line connecting the top of the plus to the bottom of the plus, and another line joining the left of the plus to the right, without the two lines crossing? On the plane, the answer is no. On a torus, the answer is yes.

Those paths of vertices of alternating colours are called Kempe chains. A biography of Kempe including his work on the four colour map theorem can be found here.

Brun’s constant and the Pentium FDIV bug

Just a quick note here ahead of a future OOMC livestream on twin primes!

You might already know that the sum $1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\dots$ diverges – it gets larger without bound, even though the terms get smaller and smaller (if not, the idea is that the terms from $\frac{1}{5}$ to $\frac{1}{8}$ add up to more than $\frac{1}{2}$, because there are four of them, and then the terms from $\frac{1}{9}$ to $\frac{1}{16}$ also add up to more than $\frac{1}{2}$, because there are eight of them, and so on; it takes a long time, but I can make this sum as large as I like by taking enough of these groups of terms). 

Perhaps surprisingly, even if you do that sum with just the prime numbers, the sum still diverges. Brun’s theorem concerns the sum with just twin primes; pairs of primes that differ by exactly 2. For each pair of twin primes, take one over each prime, and all of those together. This sum doesn’t diverge, it converges to something just a bit less than 2!

I mentioned this on the livestream because a mathematician working on this discovered the Pentium FDIV bug in the 1990s.

More chessboard problems

We suggested on the livestream that if you remove opposite corners of an 8x8 chessboard then you can cover the remaining 62 squares with dominos. You might like to check that this is true! Then you might like to think about what happens in general if two squares are removed; assuming that one is a white square and one was a black square, can you guarantee that the remaining 62 can be covered with dominoes?

Sophie also mentioned a version of the problem where you remove one square of an 8x8 chessboard (not necessarily a corner) and attempt to tile the rest with L-shaped triominos. Does it matter where the removed square was?

I’ve also seen a version where you try to tile an 8x8 chessboard (nothing removed!) with T-shaped tetrominoes. Can you tile a 10x10 chessboard with these tiles?

Peg Solitaire

There’s a game called peg solitaire (or "marble solitaire", or just "solitaire") that uses a board with holes and pegs (or marbles) that fit in the holes. It’s a game for one player. You can move a peg by jumping it over an adjacent peg if there’s a gap on the other side for it to land in. The piece that was jumped over is removed from the board.

The object of the game is to be left with one peg in the center of the board, and the starting configuration is usually for all the squares to have pegs except the middle one, but there are interesting variants where some pegs are missing, or the board is a different shape.

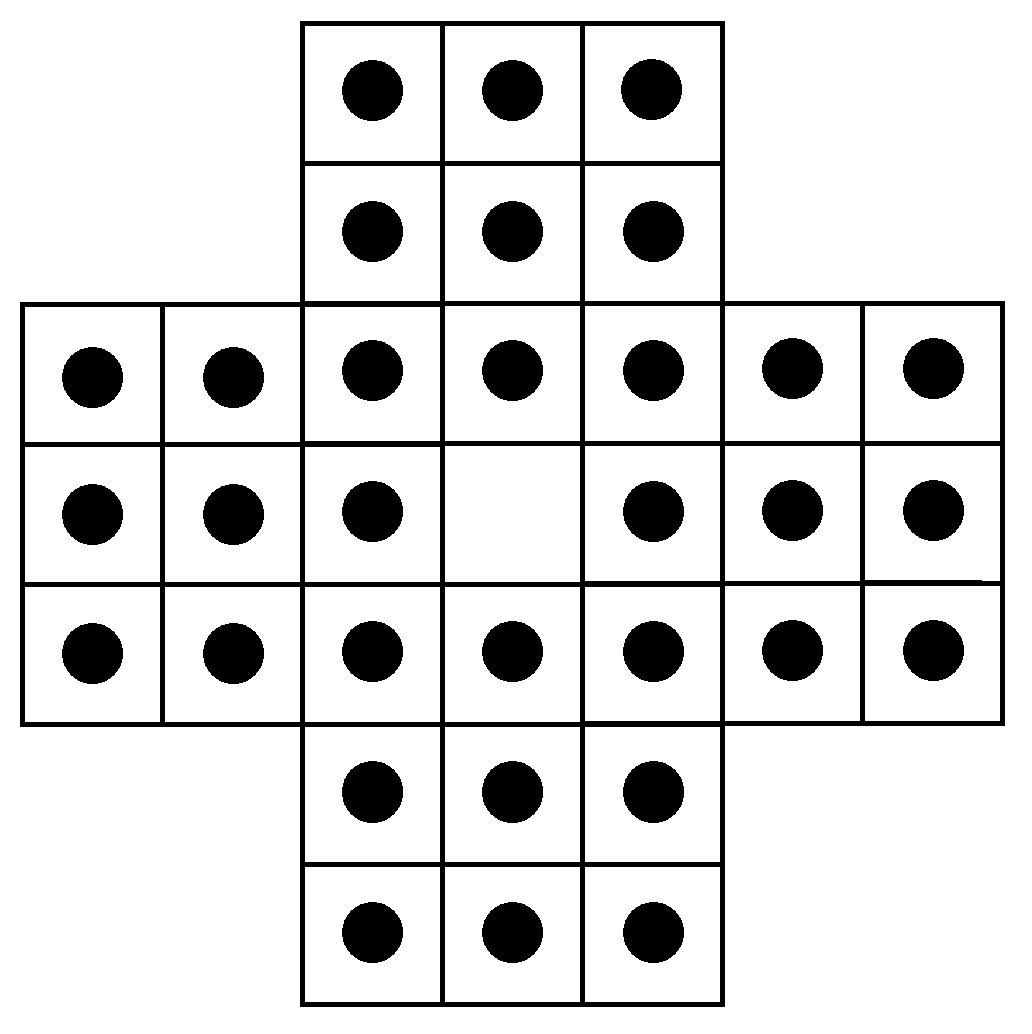
A student at Balliol recently showed me a great colouring argument for this game. We’re going to colour in diagonals, like we did with the chessboards, but in the sequence Red Red Blue, Red Red Blue, and so on.

Then each move you make does not change the parity (the even-ness or odd-ness) of the number of pegs on red squares. There are a few moves to check to convince yourself that this is true. Therefore, if the initial number of pegs on red squares is even, then the number of pegs on red squares at the end must also be even. The nice thing about this colouring is that there are six versions of it; translations and rotations of this pattern give you different restrictions on which squares the pegs start on for the puzzle to be solvable. There’s a way to combine these insights together into a super-colouring together with a rule on how to interpret the different numbers of pegs on different colours, which I’ll let you investigate yourself.