MAT 2018
This is a version of the MAT 2018 past paper, reformatted for the web. Please contact us via the link at the bottom of the page if you spot any typographical errors that have entered as a result of the reformatting.
Q1A
The area of the region bounded by the curve $y=\sqrt{x% },$ the line $y=x-2$ and the $x$-axis equals
(a) $2$
(b)$\displaystyle \frac{5}{2}$
(c) $3$
(d) $\displaystyle \frac{10}{3}$
(e) $\displaystyle \frac{16}{3}$
Q1B
The function $y=e^{kx}$ satisfies the equation \begin{equation*} \left(\frac{\mathrm{d}^2y}{\mathrm{d}x^2}+\frac{\mathrm{d}y}{\mathrm{d}x}\right)\left(\frac{\mathrm{d}y}{\mathrm{d}x}-y\right)=y\frac{\mathrm{d}y}{\mathrm{d}x} \end{equation*} for
(a) no values of $k$,
(b) exactly one value of $k$,
(c) exactly two distinct values of $k$,
(d) exactly three distinct values of $k$,
(e) infinitely many distinct values of $k$.
Q1C
Let $a, b, c$ and $d$ be real numbers. The two curves $y = ax^2+c$ and $y = bx^2 + d$ have exactly two points of intersection precisely when
(a) $\displaystyle \frac{a}{b} < 1$
(b) $\displaystyle \frac{a}{b}< \displaystyle \frac{c}{d}$
(c) $a$ < $b$
(d) $c$ < $d$
(e) $(d-c)(a-b)$ > $0$
Q1D
If $f(x) = x^2 - 5x + 7$, what are the coordinates of the minimum of $y = f(x-2)$?
(a) $\left( \displaystyle \frac{5}{2},\displaystyle\frac{3}{4} \right)$
(b) $ \left(\displaystyle \frac{9}{2},\displaystyle \frac{3}{4} \right)$
(c) $\left(\displaystyle \frac{1}{2},\displaystyle \frac{3}{4}\right)$
(d) $\left(\displaystyle \frac{9}{2},\displaystyle \frac{-5}{4}\right)$
(e) $\left(\displaystyle \frac{5}{2},\displaystyle \frac{-5}{4}\right)$
Q1E
A circle of radius 2, centred on the origin, is drawn on a grid of points with integer coordinates. Let $n$ be the number of grid points that lie within or on the circle. What is the smallest amount the radius needs to increase by for there to be $2n-5$ grid points within or on the circle?
(a)$\sqrt{5}-2$
(b) $\sqrt{6}-2$
(c) $\sqrt{8}-2$
(d) $1$
(e) $\sqrt{8}$
Q1F
A particle moves in the $xy$-plane, starting at the origin $(0,0)$. At each turn, the particle may move in one of two ways:
- it may move two to the right and one up, that is, it may be translated by the vector $(2,1)$, or
- it may move one to the right and two up, that is, it may be translated by the vector $(1,2)$.
What is the closest the particle may come to the point $\left( 25,75\right) $?
(a) $0$
(b) $5\sqrt{5}$
(c) $2\sqrt{53}$
(d) $25$
(e) $35$
Q1G
The parabolas with equations $y=x^{2}+c$ and $y^{2}=x$ touch (that is, meet tangentially) at a single point. It follows that $c$ equals
(a) $\displaystyle \frac{1}{2\sqrt{3}}$
(b) $ \displaystyle \frac{3}{4\sqrt[3]%{4}}$
(c) $ \displaystyle \frac{-1}{2}$
(d) $ \sqrt{5}-\sqrt{3}$
(e) $\sqrt{\displaystyle \frac{2}{3}}$
Q1H
Two triangles $S$ and $T$ are inscribed in a circle, as shown in the diagram below.
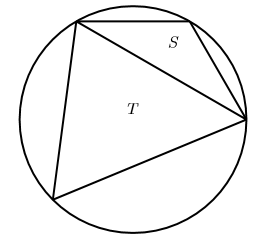
The triangles have respective areas $s$ and $t$ and $S$ is the smaller triangle so that $s< t.$ The smallest value that $\displaystyle \frac{4s^{2}+t^{2}}{5st}$ can equal is
(a) $\displaystyle \frac{2}{5}$
(b) $\displaystyle \frac{3}{5}$
(c) $\displaystyle \frac{4}{5}$
(d) $1$
(e) $\displaystyle \frac{3%}{2}$
Q1I
A sketch of the curve $(x^{8}+4yx^{6}+6y^{2}x^{4}+4y^{3}x^{2}+y^{4})^{2}=1$ is given below in
(a) 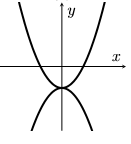
(b) 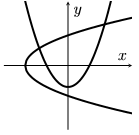
(c) 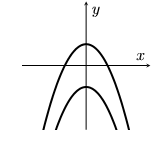
(d) 
(e) 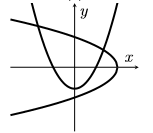
Q1J
Which of the following could be the sketch of a curve $p(x)+p(y)=0$ for some polynomial $p$?
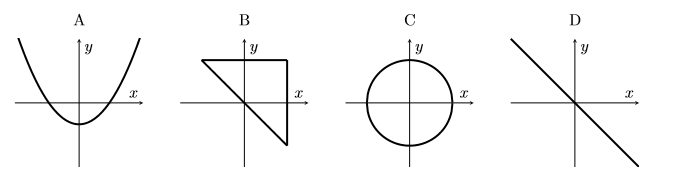
(a) A and D, but not B or C
(b) A and B, but not C or D
(c) C and D, but not A or B
(d) A, C and D, but not B
(e) A, B and C, but not D
Q2
Let $S$ and $T$ denote transformations of the $xy$-plane \begin{equation*} S(x,y)=(x+1,y), \qquad T(x,y)=(-y,x). \end{equation*}
We will write, for example, $TS$ to denote the composition of applying $S$ then $T,$ that is
\begin{equation*} TS(x,y)=T(S(x,y)), \end{equation*}
and write $T^{n}$ to denote $n$ applications of $T$ where $n$ is a positive integer.
(i) Show that $TS(x,y)\neq ST(x,y).$
(ii) For what values of $n$ is it the case that $T^{n}(x,y)=(x,y)$ for all $x,y$?
(iii) Show that applications of $S$ and $T$ in some order can produce the transformation $U(x,y)=(x-1,y).$ What is the least number of applications (of $S$ and $T$ in total) that can produce $U$? Justify your answer.
(iv) Show that for any integers $a$ and $b$ there is some sequence of applications of $S$ and $T$ that maps $(0,0)$ to $(a,b).$
(v) The parabola $C$ has equation $y=x^{2}+2x+2.$ What is the equation of the curve obtained by applying $S$ to $C$? What is the equation of the curve obtained by applying $T$ to $C$?
Q3
Let $g(x)$ be the function defined by \begin{equation*} g(x) = \begin{cases}(x-1)^2+1 &\text{ if }x \geqslant 0\\ 3-(x+1)^2 & \text{ if } x \leqslant 0,\end{cases} \end{equation*} and for $x \neq 0$ write $m(x)$ for the gradient of the chord between $(0,g(0))$ and $(x,g(x))$.
(i) Sketch the graph $y=g(x)$ for $-3\leqslant x \leqslant 3$.
(ii) Write down expressions for $m(x)$ in the two cases $x \geqslant 0$ and $x$ < $0$.
(iii) Show that $m(x)+2 = x$ for $x$ > $0$. What is the value of $m(x)+2$ when $x$ < $0$?
(iv) Explain why $g$ has derivative $-2$ at $0$.
(v) Suppose that $p$ < $q$ and that $h(x)$ is a cubic with a maximum at $x=p$ and a minimum at $x=q$. Show that $h'(x)$ < $0$ whenever $p$ < $x$ < $q$.
Suppose that $c$ and $d$ are real numbers and that there is a cubic $h(x)$ with a maximum at $x=-1$ and a minimum at $x=1$ such that $h'(0)=-3c$ and $h(0)=d$.
(vi) Show that $c$ > $0$ and find a formula for $h(x)$ in terms of $c$ and $d$ (and $x$).
(vii) Show that there are no values of $c$ and $d$ such that the graphs of $y=g(x)$ and $y=h(x)$ are the same for $-3 \leqslant x \leqslant 3$.
Q4
Consider two circles $S_1$ and $S_2$ centred at $A$ and $B$ and with radii $\sqrt{6}$ and $\sqrt{3}-1$, respectively. Suppose that the two circles intersect at two distinct points $C$ and $D$. Suppose further that the two centres $A$ and $B$ are of distance $2$ apart. The sketch below is not to scale.
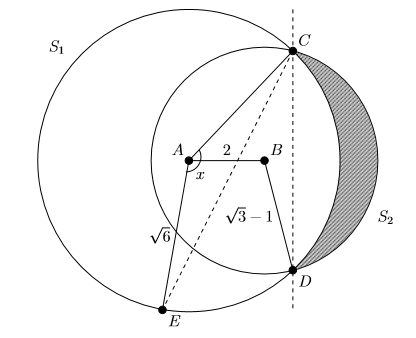
(i) Find the angle $\angle CBA$, and deduce that $A$ and $B$ lie on the same side of the line $CD$.
(ii) Show that $CD$ has length $3-\sqrt{3}$ and hence calculate the angle $\angle CAD$.
(iii) Show that the area of the region lying inside the circle $S_2$ and outside of the circle $S_1$ (that is the shaded region in the picture) is equal to \begin{equation*} \frac{\pi}{6}(5 - 4\sqrt{3}) + 3 - \sqrt{3}. \end{equation*}
(iv) Suppose that a line through $C$ is drawn such that the total area covered by $S_1$ and $S_2$ is split into two equal areas. Let $E$ be the intersection of this line with $S_1$ and $x$ denote the angle $\angle CAE$. You may assume that $E$ lies on the larger arc $CD$ of $S_1$. Write down an equation which $x$ satisfies and explain why there is a unique solution $x$.
Q5
Let $n$ be a positive integer. An $n$-brick is a rectangle of height~$1$ and width~$n$. A $1$-tower is defined as a $1$-brick. An $n$-tower, for $n \geqslant 2$, is defined as an $n$-brick on top of which exactly two other towers are stacked: a $k_1$-tower and a $k_2$-tower such that $1 \leqslant k_1 \leqslant n-1$ and $k_1 + k_2 = n$. The $k_1$-tower is placed to the left of the $k_2$-tower so that side-by-side they fit exactly on top of the $n$-brick. For example, here is a $4$-tower:
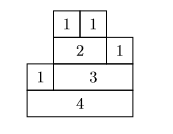
(i) Draw the four other $4$-towers.
(ii) What is the maximum height of an $n$-tower? Justify your answer.
(iii) The area of a tower is defined as the sum of the widths of its bricks. For example, the $4$-tower drawn above has area $4 + 4 + 3 + 2 = 13$. Give an expression for the area of an $n$-tower of maximum height.
(iv) Show that there are infinitely many $n$ such that there is an $n$-tower of height exactly $1 + \log_2 n$.
(v) Write $t_n$ for the number of $n$-towers. We have $t_1 = 1$. For $n \geqslant 2$ give a formula for~$t_n$ in terms of $t_k$ for $k$ < $n$. Use your formula to compute $t_6$.
(vi) Show that $t_n$ is odd if and only if $t_{2 n}$ is odd.
Q6
A positive rational number $q$ is expressed in friendly form if it is written as a finite sum of reciprocals of distinct positive integers. For example, $\displaystyle \frac4 5 = \displaystyle \frac1 2+\displaystyle \frac1 4+\displaystyle \frac1{20}$.
(i) Express the following numbers in friendly form: $\displaystyle \frac2 3$, $\displaystyle \frac2 5$, $\displaystyle \frac{23}{40}$.
(ii) Let $q$ be a rational number with $0$ < $q$ < $1$, and $m$ be the smallest natural number such than $\displaystyle \frac1 m \leqslant q$. Suppose $q = \displaystyle \frac a b$ and $\displaystyle q - \frac1 m = \frac c d$ in their lowest terms. Show that $c < a$.
(iii) Suggest a procedure by which any rational $q$ with $0$ < q < $1$ can be expressed in friendly form. Use the result in part (ii) to show that the procedure always works, generating distinct reciprocals and finishing within a finite time.
(iv) Demonstrate your procedure by finding a friendly form for $\frac4{13}$.
(v) Assuming that $\sum_{n=1}^N \displaystyle \frac1 n$ increases without bound as $N$ becomes large, show that every positive rational number can be expressed in friendly form.
Q7
A character in a video game is collecting the magic coins that are attached to a cliff face. The character starts at the bottom left corner $S$ and must reach the top right corner $E$. One point is scored for each coin $C$ that is collected on the way, and the aim is to reach the top right corner with the highest possible score. At each step the character may move either one cell to the right or one cell up, but never down or to the left.
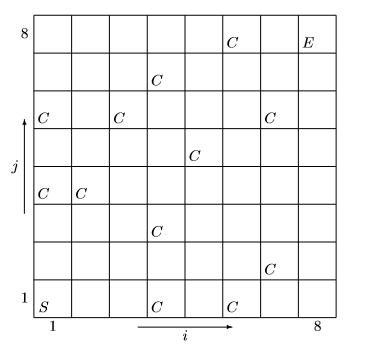
(i) Let $c(i,j) = 1$ if there is a coin at position $(i, j)$, and $c(i,j) = 0$ otherwise. Describe how the maximum score $m(i,j)$ achievable on reaching position $(i, j)$, where $i \geq 2$ and $j \geq 2$, can be determined in terms of the maximum scores $m(i,j-1)$ and $m(i-1,j)$ achievable at the positions immediate below and to the left. Briefly justify your answer.
(ii) Use the result from part (i) to fill in each cell in the diagram above to show the maximum score achievable on reaching that cell. What is the maximum score achievable in the game?
(iii) Given the array of scores $m(i,j)$, describe a method for tracing backwards from $E$ to $S$ a path that, if followed in a forward direction by the character, would achieve the maximum score. Draw one such path across the cliff.
(iv) With the pattern of coins shown, how many different paths from $S$ to $E$ achieve the maximum score? Describe a method for computing the number of such paths.

