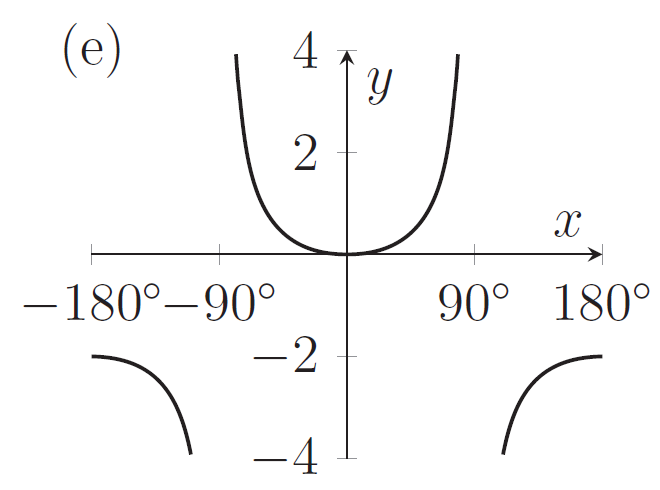MAT 2019
This is a version of the MAT 2019 past paper, reformatted for the web. Please contact us via the link at the bottom of the page if you spot any typographical errors that have entered as a result of the reformatting.
Q1A
The equation $x^3-300x=3000$ has
(a) no real solutions.
(b) exactly one real solution.
(c) exactly two real solutions.
(d) exactly three real solutions.
(e) infinitely many real solutions.
Q1B
The product of a square number and a cube number is
(a) always a square number, and never a cube number.
(b) always a cube number, and never a square number.
(c) sometimes a square number, and sometimes a cube number.
(d) never a square number, and never a cube number.
(e) always a cube number, and always a square number.
Q1C
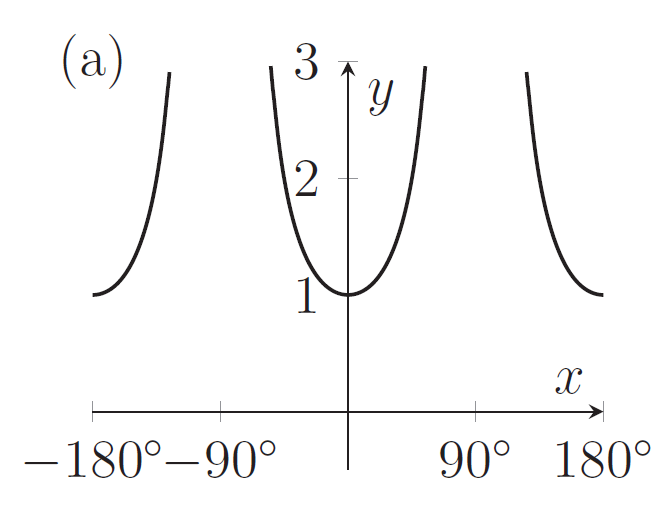
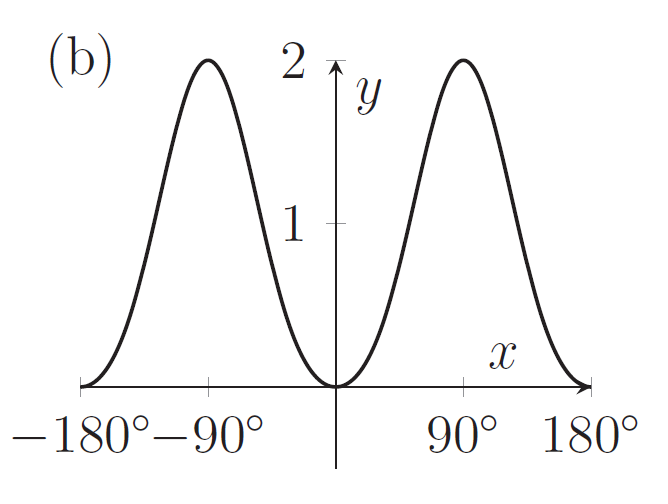
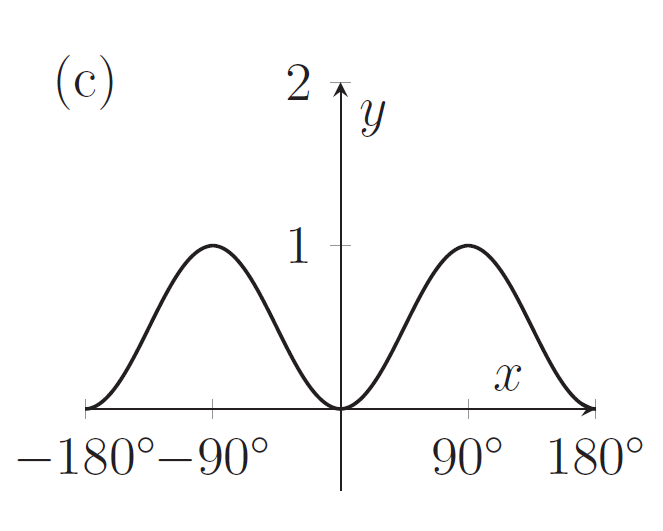
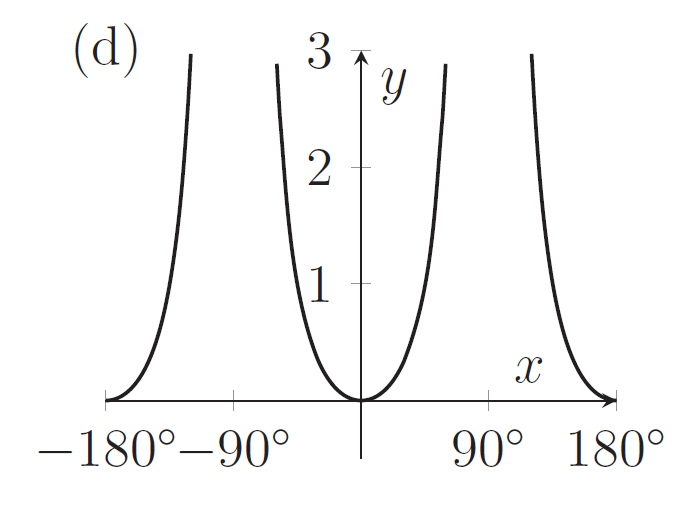
The graph of $y=\sin^2 x+\sin^4 x+\sin^6 x+\sin^8x\dots$ is sketched in
[Click or tap on images to enlarge]
Q1D
The area between the parabolas with equations $y=x^2+2ax+a$ and $y=a-x^2$ equals $9$. The possible values of $a$ are
(a) $a=1$,
(b) $a=-3$ or $a=3$,
(c) $a=-3$,
(d) $a=-1$ or $a=1$,
(e) $a=1$ or $a=3$.
Q1E
The graph of
$\sin y - \sin x = \cos^2 x - \cos^2 y$
(a) is empty.
(b) is non-empty but includes no straight lines.
(c) includes precisely one straight line.
(d) includes precisely two straight lines.
(e) includes infinitely many straight lines.
Q1F
In the interval $0<x<360^\circ$, the equation $\sin^3 x + \cos^2 x = 0$ has
(a) 0,
(b) 1,
(c) 2,
(d) 3,
(e) 4
solutions.
Q1G
Let $a,b,c>0.$ The equations $\log_a b =c$, $\log_b a =c + \frac{3}{2}$, $\log_c a =b$
(a) specify $a$, $b$ and $c$ uniquely.
(b) specify $c$ uniquely but have infinitely many solutions for $a$ and $b$.
(c) specify $c$ and $a$ uniquely but have infinitely many solutions for $b$.
(d) specify $a$ and $b$ uniquely but have infinitely many solutions for $c$.
(e) have no solutions for $a,$ $b$ and $c$.
Q1H
The triangle $ABC$ is right-angled at $B$ and the side lengths are positive numbers in geometric progression. It follows that $\tan \angle BAC$ is either
(a) $\displaystyle \sqrt{\frac{1+\sqrt{5}}{2}}$ or $\displaystyle \sqrt{\frac{1-\sqrt{5}}{2}}$,
(b) $\displaystyle \sqrt{\frac{1+\sqrt{3}}{2}}$ or $\displaystyle \sqrt{\frac{\sqrt{3}-1}{2}}$,
(c) $\displaystyle \sqrt{\frac{1+\sqrt{5}}{2}}$ or $\displaystyle \sqrt{\frac{\sqrt{5}-1}{2}}$
(d) $\displaystyle -\sqrt{\frac{1+\sqrt{5}}{2}}$ or $\displaystyle \sqrt{\frac{1+\sqrt{5}}{2}}$,
(e) $\displaystyle \sqrt{\frac{1+\sqrt{3}}{2}}$ or $\displaystyle \sqrt{\frac{1-\sqrt{3}}{2}}$.
Q1I
The positive real numbers $x$ and $y$ satisfy $0< x<y$ and $x2^x=y2^y$ for
(a) no pairs $x$ and $y$.
(b) exactly one pair $x$ and $y$.
(c) exactly two pairs $x$ and $y$.
(d) exactly four pairs $x$ and $y$.
(e) infinitely many pairs $x$ and $y$.
Q1J
An equilateral triangle has centre $O$ and side length 1. A straight line through $O$ intersects the triangle at two distinct points $P$ and $Q$. The minimum possible length of $PQ$ is
(a) $\displaystyle\frac{1}{3}$
(b) $\displaystyle\frac{1}{2}$
(c) $\displaystyle\frac{\sqrt{3}}{3}$
(d) $\displaystyle\frac{2}{3}$
(e) $\displaystyle\frac{\sqrt{3}}{2}$
Q2
For $k$ a positive integer, we define the polynomial $p_{k}(x)$ as
$p_{k}(x)=(1+x)(1+x^{2})(1+x^{3})\times \cdots \times (1+x^{k})=a_{0}+a_{1}x+\cdots +a_{N}x^{N},$
denoting the coefficients of $p_{k}(x)$ as $a_{0},\ldots ,a_{N}.$
(i) Write down the degree $N$ of $p_{k}(x)$ in terms of $k.$
(ii) By setting $x=1$, or otherwise, explain why $\displaystyle a_{\max }\geqslant \frac{2^{k}}{N+1}$ where $a_{\max }$ denotes the largest of the coefficients $a_{0},\ldots,a_{N}.$
(iii) Fix $i \geqslant 0$. Explain why the value of $a_i$ eventually becomes constant as $k$ increases.
A student correctly calculates for $k=6$ that $p_{6}(x)$ equals
$1+x+x^{2}+2x^{3}+2x^{4}+3x^{5}+4x^{6}+4x^{7}+4x^{8}+5x^{9}+5x^{10}+5x^{11}$
$+5x^{12}+4x^{13}+4x^{14}+4x^{15}+3x^{16}+2x^{17}+2x^{18}+x^{19}+x^{20}+x^{21}.$
(iv) On the basis of this calculation, the student guesses that $a_{i}=a_{N-i}$ for $0\leqslant i\leqslant N.$
By substituting $x^{-1}$ for $x,$ or otherwise, show that the student's guess is correct for all positive integers $k$.
(v) On the basis of the same calculation, the student guesses that all whole numbers in the range $1,2,\ldots ,a_{\max }$ appear amongst the coefficients $a_{0},\ldots ,a_{N}$, for all positive integers $k$.
Use part (ii) to show that in this case the student's guess is wrong. Justify your answer.
Q3
Let $a,b,m$ be positive numbers with $0<a<b.$ In the diagram below are sketched the parabola with equation $y=(x-a)(b-x)$ and the line $y=mx.$ The line is tangential to the parabola.
$R$ is the region bounded by the $x$-axis, the line and the parabola. $S$ is the region bounded by the parabola and the $x$-axis.
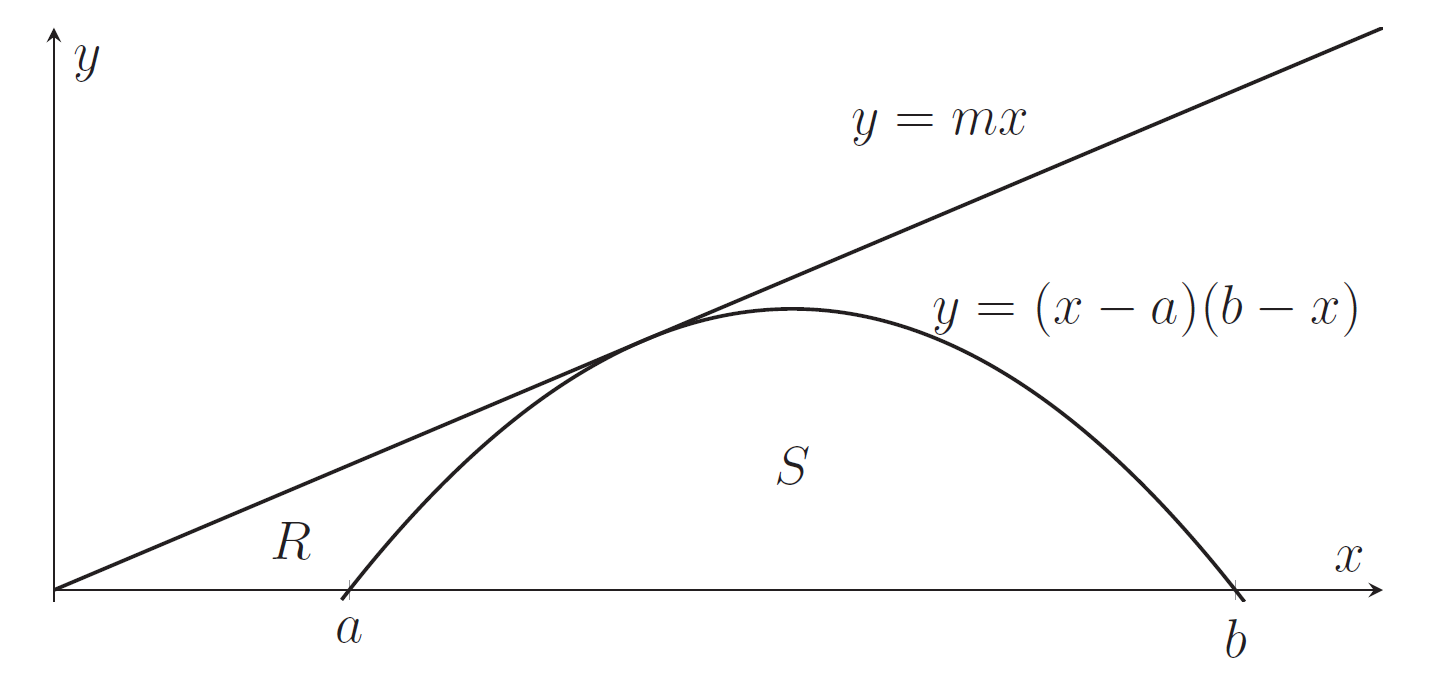
[Click or tap on image to enlarge]
(i) For $c>0,$ evaluate $\displaystyle\int_{0}^{c}x(c-x)\,\mathrm{d}x.$
Without further calculation, explain why the area of region $S$ equals $\displaystyle \frac{(b-a)^{3}}{6}.$
(ii) The line $y=mx$ meets the parabola tangentially as drawn in the
diagram. Show that $\displaystyle m=\left( \sqrt{b}-\sqrt{a}\right) ^{2}.$
(iii) Assume now that $a=1$ and write $b=\beta^2$ where $\beta>1$. Given that the area of $R$ equals $(2\beta +1)(\beta
-1)^{2}/6,$ show that the areas of regions $R$ and $S$ are equal precisely
when $(\beta -1)^{2}(\beta ^{4}+2\beta ^{3}-4\beta -2)=0. \tag{$\ast $}$
Explain why there is a solution $\beta $ to $\left( \ast \right) $ in the range $\beta >1$.
Without further calculation, deduce that for any $a>0$ there
exists $b>a$ such that the area of region $S$ equals the area of region $R.$
Q4
In this question we will consider subsets $S$ of the $xy$-plane and points $(a,b)$ which may or may not be in $S.$ We will be interested in those points of $S$ which are nearest to the point $(a,b).$ There may be many such points, a unique such point, or no such point.
(i) Let $S$ be the disc $x^{2}+y^{2}\leqslant 1$. For a given point $\left( a,b\right) $, find the unique point of $S$ which is closest to $\left( a,b\right) $.
[You will need to consider separately the cases when $a^{2}+b^{2}>1$ and when $a^{2}+b^{2}\leqslant 1.$]
(ii) Describe (without further justification) an example of a subset $S$ and a point $\left( a,b\right) $ such that there is no point of $S$ nearest to $\left( a,b\right) .$
(iii) Describe (without further justification) an example of a subset $S$ and a point $\left( a,b\right) $ such that there is more that one point of $S$ nearest to $\left( a,b\right) .$
(iv) Let $S$ denote the line with equation $y=mx+c$. Obtain an expression for the distance of $\left(a,b\right) $ from a general point $(x,mx+c)$ of $S$.
Show that there is a unique point of $S$ nearest to $\left(a,b\right) .$
(v) For some subset $S$, and for any point $\left( a,b\right) $, the nearest point of $S$ to $\left( a,b\right) $ is $ \displaystyle \left( \frac{a+2b-2}{5},\frac{2a+4b+1}{5}\right) .$
Describe the subset $S$.
(vi) Say now that $S$ has the property that "for any two points $P$ and $Q$ in $S$ the line segment $PQ$ is also in $S$". Show that, for a given point $\left( a,b\right) ,$ there cannot be two distinct points of $S$ which are nearest to $\left(a,b\right) .$
Q5
This question is about counting the number of ways of partitioning a set of $n$ elements into subsets, each with at least two and at most $n$ elements. If $n$ and $k$ are integers with $1\leq k\leq n$, let $f(n,k)$ be the
number of ways of partitioning a set of $n$ elements into $k$ such subsets. For example, $f(5, 2)=10$ because the allowable partitions of $\{1,2,3,4,5\}$ are
| $\{1,5\}, \{2,3,4\}$ | $\{1,2,5\}, \{3,4\}$ |
| $\{2,5\}, \{1,3,4\}$ | $\{3,4,5\}, \{1,2\}$ |
| $\{3,5\}, \{1,2,4\}$ | $\{1,3,5\}, \{2,4\}$ |
| $\{4,5\}, \{1,2,3\}$ | $\{2,4,5\}, \{1,3\}$ |
| $\{1,4,5\}, \{2,3\}$ | |
| $\{2,3,5\}, \{1,4\}$ |
(i) Explain why $f(n,k)=0$ if $k>n/2$.
(ii) What is the value of $f(n,1)$ and why?
(iii) In forming an allowable partition of $\{1, 2, \ldots, n+1\}$ into subsets of at least two elements, we can either
- pair $n+1$ with one other element, leaving $n-1$ elements to deal with, or
- take an allowable partition of $\{1, 2, \ldots, n\}$ and add~$n+1$ to one of the existing subsets, making a subset of size three or more.
Use this observation to find an equation for $f(n+1,k)$ in terms of $f(n-1,k-1)$ and $f(n,k)$ that holds when $2\leq k< n$.
(iv) Use this equation to compute the value of $f(7,3)$.
(v) Give a formula for $f(2n,n)$ in terms of $n$ when $n\geq 1$ and show that it is correct.
Q6
A flexadecimal number consists of a sequence of digits, with the rule that the rightmost digit must be 0 or 1, the digit to the left of it is 0, 1, or 2, the third digit (counting from the right) must be at most 3, and so on. As usual, we may omit leading digits if they are zero. We write flexadecimal numbers in angle brackets to distinguish them from ordinary, decimal numbers. Thus $ \langle 34101 \rangle $ is a flexadecimal number, but $ \langle 231 \rangle $ is not, because the digit 3 is too big for its place. (If flexadecimal numbers get very long, we will need "digits" with a value more than 9.)
The number 1 is represented by $ \langle 1 \rangle $ in flexadecimal. To add 1 to a flexadecimal number, work from right to left. If the rightmost digit $d_1$ is 0, replace it by 1 and finish. Otherwise, replace $d_1$ by 0 and examine the digit $d_2$ to its left, appending a zero at the left if needed at any stage. If $d_2 < 2$, then increase it by 1 and finish, but if $d_2 = 2$, then replace it by 0, and again move to the left. The process stops when it reaches a digit that can be increased without becoming too large. Thus, the numbers $1$ to $4$ are represented as $ \langle 1 \rangle $, $ \langle 10 \rangle $, $ \langle 11 \rangle $, $ \langle 20 \rangle $.
(i) Write the numbers from 5 to 13 in flexadecimal.
(ii) Describe a workable procedure for converting flexadecimal numbers to decimal, and explain why it works. Demonstrate your procedure by converting $ \langle 1221 \rangle $ to decimal.
(iii) Describe a workable procedure for converting decimal numbers to flexadecimal, and demonstrate it by converting 255 to flexadecimal.
(iv) We could add flexadecimal numbers by converting them to decimal, adding the decimal numbers and converting the result back again. Describe instead a procedure for addition that works directly on the digits of two flexadecimal numbers, and demonstrate it by performing the addition $ \langle 1221 \rangle + \langle 201 \rangle $.
(v) Given a flexadecimal number, how could you test whether it is a multiple of 3 without converting it to decimal?
(vi) If the $ \langle 100000 \rangle $ arrangements of the letters $\it abcdef$ are listed in alphabetical order and numbered $ \langle 0 \rangle \colon \it abcdef$, $ \langle 1 \rangle \colon \it abcdfe$, $ \langle 10 \rangle \colon \it abcedf$, etc., what arrangement appears in position $ \langle 34101 \rangle $ in the list?
Q7
You are given two identical black boxes, each with an $N$-digit display and each with two buttons marked $A$ and $B$. Button $A$ resets the display to 0, and button $B$ updates the display using a complex, unknown but fixed, function $f$, so that pressing button $A$ then repeatedly pressing button $B$ displays a fixed sequence
$x_0=0,\ x_1=f(x_0),\ x_2=f(x_1),\ \ldots,$ the same for both boxes. In general $x_i=f^i(0)$ where $f^i$ denotes
applying function $f$ repeatedly $i$ times.
You have no pencil and paper, and the display has too many digits for you to remember more than a few displayed values, but you can compare the displays on the two boxes to see if they are equal, and you can count the number of times you press each button.
(i) Explain briefly why there must exist integers $i$, $j$ with $0\leqslant i<j$ such that $x_i=x_j$.
(ii) Show that if $x_i=x_j$ then $x_{i+s}=x_{j+s}$ for any $s \geqslant 0$.
(iii) Let $m$ be the smallest number such that $x_m$ appears more than once in the sequence, and let $p > 0$ be the smallest number such that $x_m=x_{m+p}$. Show that if $i\geqslant m$ and $k\geqslant0$ then $x_{i+kp}=x_i$.
(iv) Given integers $i$, $j$ with $0 \leqslant i < j$, show that $x_i=x_j$ if and only if $i \geqslant m$ and $j-i$ is a multiple of $p$. [Hint: let $r$ be the remainder on dividing $j-i$ by $p$, and argue that $r=0$.]
(v)You conduct an experiment where (after resetting both boxes) you repeatedly press button $B$ once on one box and button $B$ twice on the other box and compare the displays, thus determining the smallest number $u > 0$ such that $x_u=x_{2u}$. What relates the value of $u$ to the (unknown) values of $m$ and $p$?
(vi) Once $u$ is known, what experiment would you perform to determine the value of $m$?
(vii) Once $u$ and $m$ are known, what experiment would tell you the value of $p$?