MAT 2020
This is a version of the MAT 2020 past paper, reformatted for the web. Please contact us via the link at the bottom of the page if you spot any typographical errors that have entered as a result of the reformatting.
Q1A
A square has centre $(3,4)$ and one corner at $(1,5)$. Another corner is at
(a) $(1,3)$,
(b) $(5,5)$,
(c) $(4,2)$,
(d) $(2,2)$,
(e) $(5,2)$.
Q1B
What is the value of $\displaystyle\int_{0}^{1}\left(e^x-x\right)\left(e^x+x\right)\,\mathrm{d}x$?
(a) $\displaystyle\frac{3e^2-2}{6}$,
(b)$\displaystyle\frac{3e^2+2}{6}$,
(c)$\displaystyle\frac{2e^2-3}{6}$,
(d) $\displaystyle\frac{3e^2-5}{6}$,
(e) $\displaystyle\frac{e^2+3}{6}$.
Q1C
The sum
\[
1-4+9-16+\dots+99^2-100^2
\]
equals
(a) $-101$
(b) $-1000$
(c) $-1111$
(d)$-4545$
(e) $-5050$.
Q1D
The largest value achieved by $3\cos^2 x+2\sin x+1$ equals
(a) $\displaystyle \frac{11}{5}$,
(b) $\displaystyle \frac{13}{3}$,
(c) $\displaystyle \frac{12}{5}$,
(d) $\displaystyle \frac{14}{9}$,
(e) $\displaystyle \frac{12}{7}$.
Q1E
A line is tangent to the parabola $y=x^2$ at the point $(a,a^2)$ where $a>0$. The area of the region bounded by the parabola, the tangent line, and the $x$-axis equals
(a) $\displaystyle \frac{a^2}{3}$,
(b) $\displaystyle \frac{2a^2}{3}$,
(c) $\displaystyle \frac{a^3}{12}$,
(d) $\displaystyle \frac{5a^3}{6}$,
(e) $\displaystyle \frac{a^4}{10}$.
Q1F
Which of the following expressions is equal to $\log_{10}(10\times9\times8\times\dots \times 2\times 1)$?
(a) $1+5\log_{10}2+4\log_{10}6$,
(b) $1+4\log_{10}2+2\log_{10}6+\log_{10}7$,
(c) $2+2\log_{10}2+4\log_{10}6+\log_{10}7$,
(d) $2+6\log_{10}2+4\log_{10}6+\log_{10}7$,
(e) $2+6\log_{10}2+4\log_{10}6$.
Q1G
A cubic has equation $y=x^3+ax^2+bx+c$ and has turning points at $(1,2)$ and $(3,d)$ for some $d$. What is the value of $d$?
(a) $-4$,
(b) $-2$,
(c) $0$,
(d) $2$,
(e) $4$.
Q1H
The following five graphs are, in some order, plots of $y=f(x)$, $y=g(x)$, $y=h(x)$, $\displaystyle y=\frac{\mathrm d f}{\mathrm{d}x}$ and $\displaystyle y=\frac{\mathrm{d}g}{\mathrm{d}x}$; that is, three unknown functions and the derivatives of the first two of those functions. Which graph is a plot of $h(x)$?
(a) 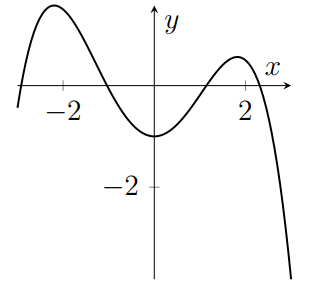
(b) 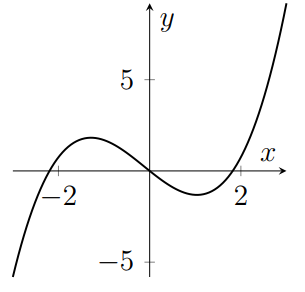
(c) 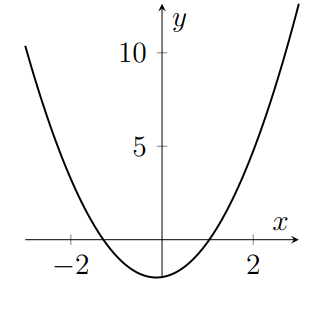
(d) 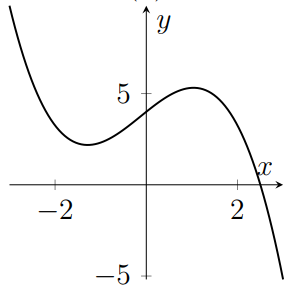
(e) 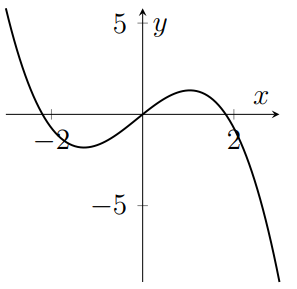
Q1I
In the range $-90^\circ<x<90^\circ$, how many values of $x$ are there for which the sum to infinity
\[
\frac{1}{\tan x}+\frac{1}{\tan^2 x}+\frac{1}{\tan^3 x}+\dots
\]
equals $\tan x$?
(a) 0,
(b) 1,
(c) 2,
(d) 3,
(e) 4.
Q1J
Consider a square with side length 2 and centre $(0,0)$, and a circle with radius $r$ and centre $(0,0)$. Let $A(r)$ be the area of the region that is inside the circle but outside the square, and let $B(r)$ be the area of the region that is inside the square but outside the circle. Which of the following is a sketch of $A(r)+B(r)$?
(a) 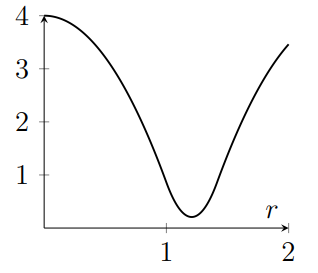
(b) 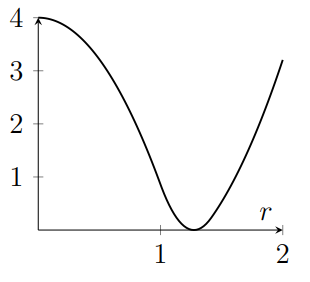
(c) 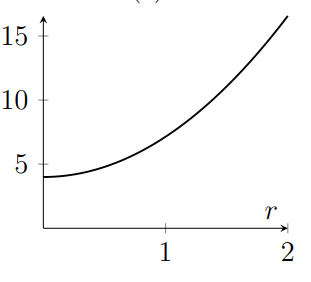
(d) 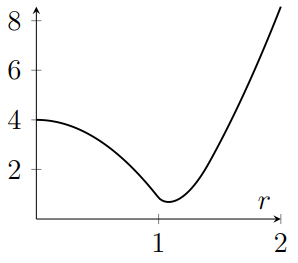
(e) 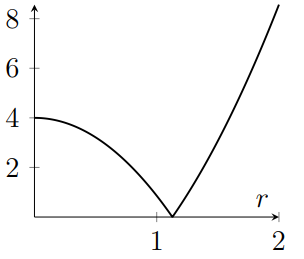
Q2
The functions $f(n)$ and $g(n)$ are defined for positive integers $n$ as follows:
\[
f(n)=2n+1,\qquad \qquad g(n)=4n.
\]
This question is about the set $S$ of positive integers that can be achieved by applying, in some order, a combination of $f$s and $g$s to the number $1$. For example as
\[
gfg(1)=gf(4)=g(9)=36,
\]
and
\[
f\!fgg(1)=f\!fg(4)=f\!f(16)=f(33)=67,
\]
then both $36$ and $67$ are in $S$.
(i) Write out the binary expansion of $100$ (one hundred).
[Recall that binary is base 2. Every positive integer $n$ can be uniquely written as a sum of powers of 2, where a given power of 2 can appear no more than once. So, for example, $13=2^{3}+2^{2}+2^{0}$ and the binary expansion of 13 is $1101$.]
(ii )Show that $100$ is in $S$ by describing explicitly a combination of $f$s and $g$s that achieves 100.
(iii) Show that $200$ is not in $S.$
(iv) Show that, if $n$ is in $S,$ then there is only one combination of applying $f$s and $g$s in order to achieve $n.$ (So, for example, 67 can only be achieved by applying $g$ then $g$ then $f$ then $f$ in that order.)
(v) Let $u_{k}$ be the number of elements $n$ of $S$ that lie in the range $2^{k}\leqslant n<2^{k+1}.$ Show that
\[
u_{k+2}=u_{k+1}+u_{k}
\]
for $k\geqslant 0.$
(vi) Let $s_{k}$ be the number of elements $n$ of $S$ that lie in the range $1\leqslant n<2^{k+1}.$ Show that
\[s_{k+2}=s_{k+1}+s_{k}+1\]
for $k\geqslant 0.$
Q3
Below is a sketch of the curve $S$ with equation $y^{2}-y=x^{3}-x$. The curve crosses the $x$-axis at the origin and at $(a,0)$ and at $(b,0)$ for some real numbers $a<0$ and $b>0$. The curve only exists for $\alpha\leq x \leq \beta$ and for $x\geq \gamma$. The three points with coordinates $(\alpha,\delta)$, $(\beta,\delta)$, and $(\gamma, \delta)$ are all on the curve.
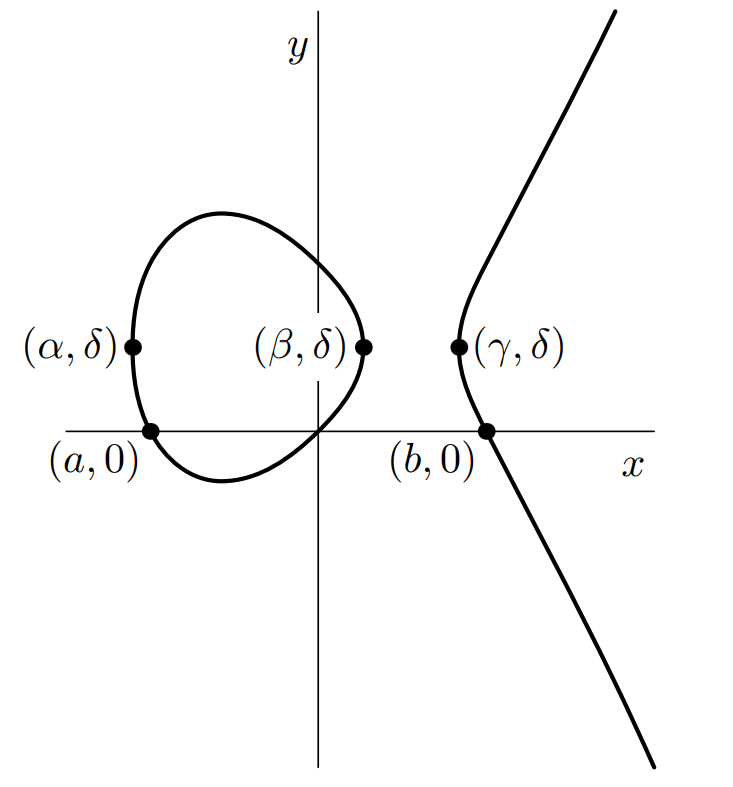
(i) What are the values of $a$ and $b$?
(ii) By completing the square, or otherwise, find the value of $\delta $.
(iii) Explain why the curve is symmetric about the line $y=\delta$.
(iv) Find a cubic equation in $x$ which has roots $\alpha ,\beta ,\gamma$. (Your expression for the cubic should not involve $\alpha$, $\beta$, or $\gamma$). Justify your answer.
(v) By considering the factorization of this cubic, find the value of $\alpha +\beta +\gamma.$
(vi) Let $C$ denote the circle which has the points $(\alpha,\delta )$ and $(\beta ,\delta )$ as ends of a diameter. Write down the equation of $C$. Show that $C$ intersects $S$ at two other points and find their common $x$-co-ordinate in terms of $\gamma$.
Q4
(i) A function $f(x)$ is said to be even if $f(-x)=f(x)$ for all $x$. A function is said to be odd if $f(-x)=-f(x)$ for all $x.$
(a) What symmetry does the graph $y=f(x)$ of an even function have?
What symmetry does the graph $y=f(x)$ of an odd function have?
(b) Use these symmetries to show that the derivative of an even function is an odd function, and that the derivative of an odd function is an even function.
[You should not use the chain rule.]
(ii) For $-45^{\circ }<\theta <45^{\circ }$, the line $L$ makes an angle $\theta $ with the line $y=x$ as drawn in the figure below. Let $A(\theta )$ denote the area of the triangle which is bounded by the $x$-axis, the line $x+y=1$ and the line $L.$
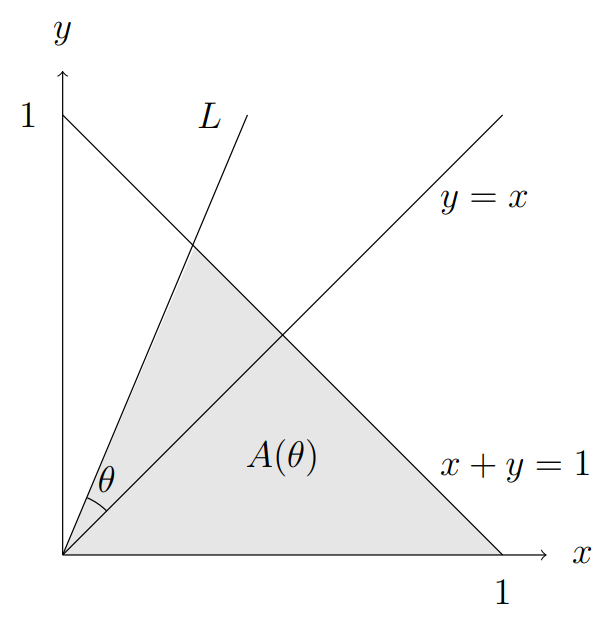
(a) Let $0<\theta <45^{\circ }.$ Arguing geometrically, explain why \[A(\theta )+A(-\theta )=\frac{1}{2}.
\]
(b) For $0<\theta <45^{\circ }$, determine a formula for $A(\theta ).$
(c) Sketch the graph of $A(\theta )$ against $\theta $ for $-45^{\circ }<\theta <45^{\circ }.$
(d) In light of the identity in part (ii)(a), what symmetry does the graph of $A(\theta )$ have?
(e) Without explicitly differentiating, explain why $\displaystyle \frac{\mathrm{d}^{2}A}{\mathrm{d}\theta ^{2}}=0$ when $\theta =0.$
Q5
Miriam and Adam agree to relieve the boredom of the school holidays by eating sweets, but their mother insists they limit their consumption by obeying the following rules.
- Miriam eats as many sweets on any day as there have been sunny days during the holiday so far, including the day in question.
- Adam eats sweets only on rainy days. If day $k$ of the holiday is rainy, then he eats $k$ sweets on that day.
For example, if the holiday is eight days long, and begins Rainy, Sunny, Sunny, ... , then the tally of sweet consumption might look like this:
| Day | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Total |
| Weather | R | S | S | R | R | S | S | R | |
| Miriam | 0 | 1 | 2 | 2 | 2 | 3 | 4 | 4 | 18 |
| Adam | 1 | 0 | 0 | 4 | 5 | 0 | 0 | 8 | 18 |
In this case, Miriam and Adam eat the same number of sweets in total.
(i) If the holiday has 30 days, 15 of which are sunny and 15 rainy, what arrangement of sunny and rainy days would lead Miriam to eat the greatest number of sweets in total, and what arrangement would lead to the least number? Give the number of sweets that Miriam eats in each case.
(ii) Show that, in the two cases mentioned in part (i), Adam eats the same number of sweets as Miriam.
(iii) Suppose, in a sequence of sunny and rainy days, we arrange to swap a rainy day with a sunny day that immediately follows it. How does the total number of sweets eaten by Miriam change when we make the swap? What about the total number of sweets eaten by Adam?
(iv) If the holiday has 15 sunny days and 15 rainy days, must Miriam and Adam eat the same number of sweets in total? Explain your answer.
Q6
The cancellation of the Wimbledon tournament has led to a world surplus of tennis balls, and Santa has decided to use them as stocking fillers. He comes down the chimney with $n$ identical tennis balls, and he finds $k$ named stockings waiting for him.
Let $g(n,k)$ be the number of ways that Santa can put the $n$ balls into the $k$ stockings; for example, $g(2,2)=3$, because with two balls and two children, Miriam and Adam, he can give both balls to Miriam, or both to Adam, or he can give them one ball each.
(i) What is the value of $g(1, k)$ for $k\geq 1$?
(ii) What is the value of $g(n, 1)$?
(iii) If there are $n\geq 2$ balls and $k\geq 2$ children, then Santa can either give the first ball to the first child, then distribute the remaining balls among all $k$ children, or he can give the first child none, and distribute all the balls among the remaining children. Use this observation to formulate an equation relating the value of $g(n, k)$ to other values taken by $g$.
(iv) What is the value of $g(7, 5)$?
(v) After the first house, Rudolf reminds Santa that he ought to give at least one ball to each child. Let $h(n, k)$ be the number of ways of distributing the balls according to this restriction. What is the value of $h(7, 5)$?
Q7
Quantiles is game for a single player. It is played with an inexhaustible supply of tiles, each bearing one of the symbols $A$, $B$, or $C$. In each move, the player lays down a row of tiles containing exactly one $A$ and one $B$, but varying numbers of $C$'s.
The rules are as follows:
- The player may play the basic rows $CACBCC$ and $CCACBCCC$.
- If the player has already played rows of the form $rAsBt$ and $xAyBz$ (they may be the same row), where each of $r$, $s$, $t$, $x$, $y$, $z$ represents a sequence of $C$'s, then he or she may add the row $rxAsyBtz$, in which copies of the sequences of $C$'s from the previous rows are concatenated with an intervening $A$ and $B$: this is called a join move. The original rows remain, and may be used again in subsequent join moves.
- No other rows may be played.
The player attempts to play one row after another so as to finish with a specified goal row.
(i) Give two examples of rows, other than basic rows, that may be played in the game.
(ii) Give two examples of rows, each containing exactly one $A$ and one $B$, that may never be played, and explain why.
(iii) Let $C^n$ denote an unbroken sequence of $n$ tiles each labelled with $C$. Can the goal row $C^{64}AC^{48}BC^{112}$ be achieved? Justify your answer.
(iv) Can the goal row $C^{128}AC^{48}BC^{176}$ be achieved? Justify your answer.
(v) The goal row $C^{31}AC^{16}BC^{47}$ is achievable; show that it can be reached with 7 join moves.
(vi) In any game, we call a row useless if it repeats an earlier row or it is not used in a subsequent join move. What is the maximum number of join moves in a game that ends with $C^{31}AC^{16}BC^{47}$ and contains no useless rows?

