MAT 2021
This is a version of the MAT 2021 past paper, reformatted for the web. Please contact us via the link at the bottom of the page if you spot any typographical errors that have entered as a result of the reformatting.
Q1A
A regular dodecagon is a 12-sided polygon with all sides the same length and all internal angles equal. If I construct a regular dodecagon by connecting 12 equally-spaced points on a circle of radius 1, then the area of this polygon is
(a) $6+3\sqrt{3}$,
(b) $2\sqrt{2}$,
(c) $3\sqrt{2}$,
(d) $3\sqrt{3}$,
(e) $3$.
Q1B
The positive number $a$ satisfies $$\int_{0}^{a}\left(\sqrt{x}+x^2\right)\,\mathrm{d}x=5$$ if
(a) $a=\left(\sqrt{21}-1\right)^{1/3}$,
(b) $a=\sqrt{3}$,
(c) $a=3^{2/3}$,
(d) $a=(\sqrt{6}-1)^{2/3}$,
(e) $a=5^{2/3}$.
Q1C
Tangents to $y=e^x$ are drawn at $(p,e^p)$ and $(q,e^q)$. These tangents cross the $x$-axis at $a$ and $b$ respectively. It follows that, for all $p$ and $q$,
(a) $pa=qb$,
(b) $p-a<q-b$,
(c) $p-a=q-b$,
(d) $p-a>q-b$,
(e) $p+q=a+b$.
Q1D
The area of the region bounded by the curve $y=e^x$, the curve $y=1-e^x$, and the $y$-axis equals
(a) $0$,
(b) $1-\ln 2$,
(c) $\frac{1}{2}-\frac{1}{2}\ln 2$,
(d) $\ln 2 -1$,
(e) $1-\ln\frac{1}{2}$.
[Note that $\ln x$ is alternative notation for $\log_e x$.]
Q1E
Six vectors $\textbf{v}_1$, $\textbf{v}_2$, $\textbf{v}_3$, $\textbf{v}_4$, $\textbf{v}_5$, $\textbf{v}_6$ are each chosen to be either $\displaystyle \left(\begin{matrix}1\\1\end{matrix}\right)$ or $\displaystyle \left(\begin{matrix}3\\2\end{matrix}\right)$ with equal probability, with each choice made independently. The probability that the sum $\textbf{v}_1+\textbf{v}_2+\textbf{v}_3+\textbf{v}_4+\textbf{v}_5+\textbf{v}_6$ is equal to the vector $\displaystyle \left(\begin{matrix}10\\8\end{matrix}\right)$ is
(a) $0$,
(b) $\displaystyle\frac{3}{64}$,
(c) $\displaystyle\frac{15}{64}$,
(d) $\displaystyle\frac{1}{6}$,
(e) $\displaystyle\frac{5}{16}$.
Q1F
The tangent to the curve $y=x^3-3x$ at the point $(a,a^3-3a)$ also passes through the point $(2,0)$ for precisely
(a) no values of $a$,
(b) one value of $a$,
(c) two values of $a$,
(d) three values of $a$,
(e) all values of $a$.
Q1G
The sum
\begin{equation*}
\sin^2 (1^\circ) + \sin^2 (2^\circ) + \sin^2 (3^\circ) +\dots+ \sin^2 (89^\circ) +\sin^2 (90^\circ)
\end{equation*}
is equal to
(a) $44$,
(b) $44\frac{1}{2}$,
(c) $45$,
(d) $45 \frac{1}{2}$,
(e) $46$.
Q1H
Which of the following graphs shows
\begin{equation*}
y=\log_2\left(9-8\sin x-6\cos^2 x\right)
\end{equation*}
in the range $0\leq x\leq 360^\circ$?
(a)
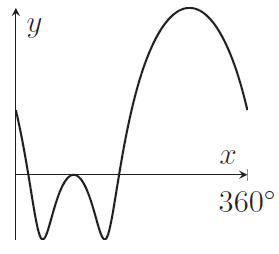
(b)
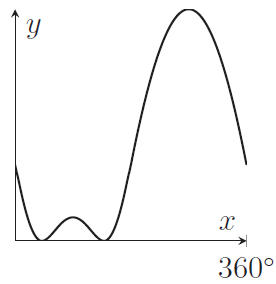
(c)
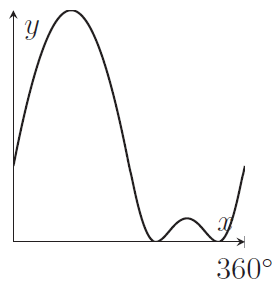
(d)
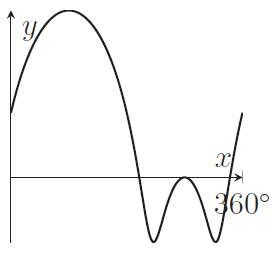
(e)
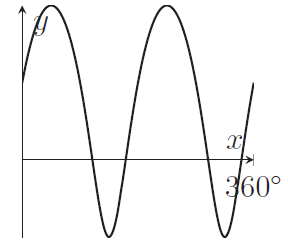
Q1I
A sequence is defined by $a_0=2$ and then for $n\geq 1$, $a_n$ is one more than the product of all previous terms (so $a_1=3$ and $a_2=7$, for example). It follows that for all $n\geq 1$,
(a) $a_n=4a_{n-1}-5$,
(b) $a_n=a_{n-1}\left(a_{n-1}-1\right)+1$,
(c) $a_n=2a_{n-1}(a_{n-1}-3)+7$,
(d) $\displaystyle a_{n}=\frac{3}{2}n^2-\frac{1}{2}n+2$,
(e) None of the above.
Q1J
Four distinct real numbers $a$, $b$, $c$, and $d$ are used to define four points $$A=(a,b), \quad B=(b,c),\quad C=(c,d),\quad D=(d,a).$$
The quadrilateral $ABCD$ has all four sides the same length
(a) if and only if $(a-b)^2=(c-d)^2$,
(b) if and only if $(a-c)^2=(b-d)^2$,
(c) if and only if $(a-d)^2=(b-c)^2$,
(d) if and only if $a-b+c-d=0$,
(e) for no values of $a$, $b$, $c$, $d$.
Q2
In this question you may use without proof the following fact:
\begin{equation*}
\ln (1-x)=-x-\frac{x^2}{2}-\frac{x^3}{3}-\frac{x^4}{4}\dots-\frac{x^n}{n}\dots \quad\text{for any $x$ with $|x|<1$.}
\end{equation*}
[Note that $\ln x$ is alternative notation for $\log_e x$.]
(i) By choosing a particular value of $x$ with $|x|<1$, show that
\begin{equation*}
\ln 2= \frac{1}{2}+\frac{1}{2\times 2^2}+\frac{1}{3\times 2^3}+\frac{1}{4\times 2^4}+\frac{1}{5\times 2^5}+\dots .
\end{equation*}
(ii) Use part (i) and the fact that
\begin{equation*}
\frac{1}{n2^n}<\frac{1}{3\times 2^{n}}\quad\text{for $n\geq 4$}
\end{equation*}
to find the integer $k$ such that $\displaystyle \frac{k}{24} < \ln 2 < \frac{k+1}{24}$.
(iii) Show that $$\ln\left(\frac{3}{2}\right)=\frac{1}{2}-\frac{1}{2\times 2^2}+\frac{1}{3\times 2^3}-\frac{1}{4\times 2^4}+\frac{1}{5\times 2^5}-\dots .$$ and deduce that
\begin{equation*}
\ln 3=1+\frac{1}{3\times 2^2}+\frac{1}{5\times 2^4}+\frac{1}{7\times 2^6}+\dots.
\end{equation*}
(iv) Deduce that $\displaystyle \frac{13}{12} <\ln 3< \frac{11}{10}$.
(v) Which is larger: $3^{17}$ or $4^{13}$? Without calculating either number, justify your answer.
Q3
The degree of a polynomial is the highest exponent that appears among its terms. For example, $2x^6-3x^2+1$ is a polynomial of degree 6.
(i) A polynomial $p(x)$ has a turning point at $(0,0)$. Explain why $p(0)=0$ and why $p'(0)=0$, and explain why there is a polynomial $q(x)$ such that
\begin{equation*}
p(x)=x^2q(x).\tag{$\ast$}
\end{equation*}
(ii) A polynomial $r(x)$ has a turning point at $(a,0)$ for some real number $a$. Write down an expression for $r(x)$ that is of a similar form to the expression ($\ast$) above. Justify your answer in terms of a transformation of a graph.
(iii) You are now given that $f(x)$ is a polynomial of degree 4, and that it has two turning points at $(a,0)$ and at $(-a,0)$ for some positive number $a$.
(a) Write down the most general possible expression for $f(x)$. Justify your answer.
(b) Describe a symmetry of the graph of $f(x)$, and prove algebraically that $f(x)$ does have this symmetry.
(c) Write down the $x$-coordinate of the third turning point of $f(x)$.
(iv) Is there a polynomial of degree 4 which has turning points at $(0,0)$, at $(1,3)$, and at $(2,0)$? Justify your answer.
(v) Is there a polynomial of degree 4 which has turning points at $(1,6)$, at $(2,3)$, and at $(4,6)$? Justify your answer.
Q4
Charlie is trying to cut a cake. The cake is a square with side length 2, and its corners are at $(0,0)$, $(2,0)$, $(2,2)$, and $(0,2)$. Charlie's first cut is a straight line segment from the point $(x,y)$ to $(x,0)$, where $0\leq x \leq 2$ and $0 \leq y \leq 2$.
Charlie plans to make a second straight cut from the point $(x,y)$ to a point $(0,k)$ somewhere on the left-hand edge of the cake. This will make a slice of cake which is bounded to the left of the first cut and bounded below the second cut.
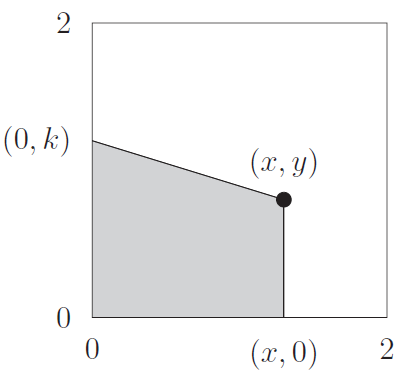
(i) Find the area of the slice of cake in terms of $x$, $y$, and $k$. Check your expression by verifying that if $x=1$ and $y=1$, then choosing $k=1$ gives a slice of cake with area 1.
(ii) Find another point $(x,y)$ on the cake such that choosing $k=1$ gives a slice of cake with area 1.
(iii) Show that it is only possible to choose a value of $k$ that gives a slice of cake with area 1 if both $xy\leq 2$ and $x(2+y) \geq 2$.
(iv) Sketch the region $R$ of the cake for which both inequalities in part (iii) hold, indicating any relevant points on the edges of the cake.
(v) Charlie may instead plan to make the second straight cut from $(x,y)$ to a point $(m,2)$ on the top edge of the cake in order to make a slice bounded to the left of the two cuts. Find two necessary and sufficient inequalities for $x$ and $y$ which must both hold in order for this to give a slice of area 1 for some value of $m$. Sketch the region of the cake for which both inequalities hold.
Q5
A triangular triple is a triple of positive integers $(a, b, c)$ such that we can construct a triangle with sides of length $a$, $b$ and $c$. This means that the sum of any two of the numbers is strictly greater than the third; so if $a \leq b \leq c$, then it is equivalent to requiring $a + b > c$. For example, $(3, 3, 3)$ and $(4, 5, 3)$ are triangular triples, but $(1, 3, 2)$ and $(3, 3, 6)$ are not. For any positive integer $P$, we define $f(P)$ to be the number of triangular triples such that the perimeter $a + b + c$ is equal to $P$. Triples with the same numbers, but in a different order, are counted as being distinct. So $f(12) = 10$, because there are $10$ triangular triples with perimeter $12$, shown below:
| $(3, 4, 5)$ | $(3,5,4)$ | $(4, 3, 5)$ | $(4, 5, 3)$ | $(5, 3, 4)$ | $(5, 4, 3)$ |
| $(2, 5, 5)$ | $(5, 2, 5)$ | $(5, 5, 2)$ | |||
| $(4, 4, 4)$ |
(i) Write down the values of $f(3)$, $f(4)$, $f(5)$ and $f(6)$.
(ii) If $(a, b, c)$ is a triangular triple, show that $(a + 1, b + 1, c + 1)$ is also a triangular triple.
(iii) If $(x, y, z)$ is a triangular triple, with $x + y + z$ equal to an even number greater than or equal to $6$, show that each of $x, y, z$ is at least $2$ and that $(x - 1, y - 1, z-1)$ is also a triangular triple.
(iv) Using the previous two parts, prove that for any positive integer $k \geq 3$,
\[ f(2k - 3) = f(2k). \]
(v) We will now consider the case where $P \geq 6$ is even, and we will write $P = 2S$.
(a) Show that in this case $(a, b, c)$ is a triangular triple with $a + b + c = P$ if and only if each of $a$, $b$, $c$ is strictly smaller than $S$.
(b) For any $a$ such that $2 \leq a \leq S-1$, show that the number of possible values of $b$ such that $(a, b, P - a - b)$ is a triangular triple is $a-1$. Hence find an expression for $f(P)$ for any even $P \geq 6.$
(vi) Find $f(21)$.
Q6
Distinct numbers are arranged in an $m \times n$ rectangular table with $m$ rows and $n$ columns so that in each row the numbers are in increasing order (left to right), and in each column the numbers are in increasing order (top to bottom). Such a table is called a sorted table and each location of the table containing a number is called a cell. Two examples of sorted tables with $3$ rows and $4$ columns (and thus $3 \times 4 = 12$ cells) are shown below.
| 3 | 12 | 33 | 64 |
| 15 | 26 | 37 | 78 |
| 19 | 40 | 51 | 92 |
| 5 | 22 | 53 | 68 |
| 18 | 36 | 67 | 78 |
| 19 | 45 | 81 | 92 |
We index the cells of the table with a pair of integers $(i, j)$, with the top-left corner being $(1, 1)$ and the bottom-right corner being $(m, n)$. Observe that the smallest entry in a sorted table can only occur in cell $(1, 1)$; however, note that the second smallest entry can appear either in cell $(1, 2)$, as in the first example above, or in cell $(2, 1)$ as in the second example above.
(i)(a) Assuming that $m, n\geq 3$, where in an $m \times n$ sorted table can the third-smallest entry appear?
(b) For any $k \geq 4$ satisfying $m, n \geq k$, where in an $m\times n$ sorted table can the $k^{\text{th}}$ smallest entry appear? Justify your answer.
(ii) Given an $m \times n$ sorted table, consider the problem of determining whether a \text{particular} number $y$ appears in the table. Outline a procedure that inspects at most $m + n - 1$ cells in the table, and that correctly determines whether or not $y$ appears in the table. Briefly justify why your procedure terminates correctly in no more than $m + n - 1$ steps.
[Hint: As the first step, consider inspecting the top-right cell.]
(iii) Consider an $m \times n$ table, say $A$, which might not be sorted; an example is shown below. Obtain table $B$ from $A$ by re-arranging the entries in each row so that they are in sorted order. Then obtain table $C$ from $B$ by re-arranging the entries in each column so that they are in sorted order. Fill in tables $B$ and $C$ here:
A:
| 33 | 92 | 46 | 24 |
| 25 | 26 | 37 | 8 |
| 49 | 40 | 81 | 22 |
B:
C:
(iv) Show that for any $m \times n$ table $A$, performing the two operations from part (iii) results in a sorted table $C$.
Q7
Throughout this question, all functions will be Boolean functions of Boolean input variables. A Boolean variable can be either $0$ or $1$. A Boolean function may have one or more Boolean input variables, and the output of a Boolean function is also either $0$ or $1$. Three elementary Boolean functions are defined as follows:
- The function $\textbf{min}(x_1, \ldots, x_k)$ can take any number of inputs. It outputs the value $1$ exactly when each of its inputs is $1$, that is the output of the function is the minimum value among its inputs.
- The function $\textbf{max}(x_1, \ldots, x_k)$ can take any number of inputs. It outputs the value $1$ exactly when at least one of its inputs is $1$, that is the output of the function is the maximum value among its inputs.
- The function $\textbf{flip}$ takes a single input and is defined as $\textbf{flip}(x_1) = 1 - x_1$.
First we will consider Boolean functions obtained by combining the three elementary Boolean functions. One such function is shown below:
\[ f(x_1, x_2, x_3) = \textbf{min}(\textbf{max}(x_1, x_2, x_3), \textbf{flip}(\textbf{min}(x_1, x_2, x_3))). \]
(i) Describe in words when the function $f$ outputs $1$ and when it outputs $0$.
(ii) The function $\textbf{majority}(x_1, \ldots, x_k)$ takes $k$ inputs and outputs $1$ exactly when strictly greater than $k/2$ of its inputs are $1$. Explain how you could combine elementary Boolean functions to obtain the following functions:
(a) $\textbf{majority}(x_1, x_2)$
(b) $\textbf{majority}(x_1, x_2, x_3)$
Now we will consider Boolean functions that can be obtained by combining only $\textbf{majority}$ functions.
(iii) There are exactly $16$ distinct Boolean functions of two input variables. Some of these can be represented using only $\textbf{majority}$ functions that take $3$ inputs; the use of $0$ or $1$ as fixed inputs to $\textbf{majority}$ is permitted. For example, $\textbf{majority}(x_1, x_2, 1)$ represents the function $\textbf{max}(x_1, x_2)$.
Find any four other Boolean functions of two variables that can be represented by combining one or more $\textbf{majority}$ functions of $3$ inputs. Write your answers in terms of $\textbf{majority}$ functions.
(iv) Give an example of a Boolean function $g$ of two input variables that cannot be represented by combining $\textbf{majority}$ functions (of any number of inputs). You should write your answer by explicitly specifying $g(0,0)$, $g(0, 1)$, $g(1, 0)$ and $g(1, 1)$. Justify your answer.
In the last part, you may express Boolean functions by combining any of the elementary Boolean functions or the $\textbf{majority}$ function.
(v) Consider four input variables $x_1, x_2, x_3, x_4$. Let $z_1 = \textbf{min}(x_1, x_2)$, $z_2 = \textbf{min}(x_2, x_3)$, $z_3 = \textbf{min}(x_3, x_4)$, $z_4 = \textbf{min}(x_4, x_1)$. It is sometimes possible to represent a function $s(x_1, x_2, x_3, x_4)$ using a function $t(z_1, z_2, z_3, z_4)$. For example, $\textbf{min}(x_1, x_2, x_3, x_4) = \textbf{min}(z_1, z_2, z_3, z_4)$, as both functions output $1$ if and only if all four $x_i$ are $1$.
Can you represent the following functions of inputs $x_1, x_2, x_3, x_4$ as some Boolean function of inputs $z_1, z_2, z_3, z_4$? Justify your answers
(a) $\textbf{majority}(x_1, x_2, x_3, x_4)$.
(b) The function $\textbf{parity}(x_1, x_2, x_3, x_4)$ which outputs $1$ exactly when an odd number of its inputs are $1$.

