The Clebsch Diagonal Surface
The 27 Lines
In 1849, the English mathematicians Arthur Cayley and George Salmon made the remarkable discovery that every smooth cubic surface in $\mathbb{P}^3$ over $\mathbb{C}$ contains exactly 27 lines [1]. This sparked a growth of interest in the study of cubic surfaces, leading to work which inspired some of our models.
We say points in projective space are "real" or "complex" in the sense that their coordinates are purely real numbers or, respectively, if they are complex. The 27 lines on a cubic are often complex, so are not easily visualised. Indeed, $\mathbb{P}^3$ defined over $\mathbb{C}$ has effectively six (real) dimensions, plus a plane at infinity. However, it is possible for all 27 of a cubic surface's lines to be real, and a very elegant cubic displaying this property was discovered in 1871 by Prussian mathematician Alfred Clebsch [2]. The Clebsch diagonal surface has the property that all 27 of its lines are real. Model VII 1 represents this surface.
Double-Sixes
The intersections of the 27 lines on the Clebsch diagonal surface have an interesting configuration. In 1858, Swiss mathematician Ludwig Schläfli studied their behaviour [3], introducing the notion of a "double-six". A double-six is a collection of 12 of the 27 lines on a cubic, denoted by Schläfli as below:
$$\left( \begin{matrix}a_{1,1} & a_{1,2} & a_{1,3} & a_{1,4} & a_{1,5} & a_{1,6}\a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4} & a_{2,5} & a_{2,6}nd{matrix} ight) $$
The double-six has the property that each line {i,j}$ meets exactly the 5 lines of the form {k,l}$ where eq k$ and eq l$, yielding a total of 30 intersection points. Smooth cubics (those without singularities) have 36 double-sixes. On model VII nr.1 we can see 12 lines forming a double-six which are coloured red and green. Their configuration is described by taking the green lines to be {1,1}, a_{1,2}, a_{1,3}, a_{1,4}, a_{1,5}, a_{1,6}$ and the red lines to be {2,1}, a_{2,2}, a_{2,3}, a_{2,4}, a_{2,5}, a_{2,6}$. On the model, we can see each of these lines meeting four other lines of the other colour, with the fifth intersection occuring below the range of the model [6]. Owing to its symmetry, the Clebsch cubic has many nice symmetry properties. For example Schläfli also proved that the remaining 15 lines meet the double-six with a nice configuration [7].
Schläfli was the first to study cubic surfaces over the reals (i.e. disregard the complex points, looking only at the real points), and classified real cubics by their number of real lines and real "tritangent planes" [3]. A tritangent plane to a smooth cubic is a plane which intersects the surface in three lines, which themselves must all meet forming a triangle (see images in Hunt's paper [4]). Schläfli showed that on a smooth, real cubic the number of real lines and respectively real tritangent planes must be one of the following combinations: $(27, 15), (15, 15), (7, 5), (3, 13), (3, 7)$. Such clean structure does not occur in general for cubics with singularities.
There is an unusual numbering system applied to the remaining 15 lines on the Clebsch surface, which are all coloured black. Rather than consecutive integers, we have 12, 13, 14, 15, 16, 23, 24, 25, 26, 34, 35, 36, 45, 46, 56. This is easily understood when we consider the pairs of digits involved. Line number 12 passes through the two tritangent planes spanned by the pairs of lines $(1, 2')$ and $(1', 2)$. Similarly for the others: line $ passes through the two planes spanned by $(a, b')$ and $(a', b)$.
Defining Equations
In $\mathbb{P}^4$, with homogeneous co-ordinates {0}, x_{1}, x_{2}, x_{3}, x_{4}$, the Clebsch surface is defned by the equations ${0} + x_{1} + x_{2} + x_{3} + x_{4} = 0,\; x_{0}^3 + x_{1}^3 + x_{2}^3 + x_{3}^3 + x_{4}^3 = 0$$ By eliminating {0}$ from these equations, we see that it is in fact isomorphic to (i.e. has the same geometric structure as) the surface in $\mathbb{P}^3$ defined by ${1}^3 + x_{2}^3 + x_{3}^3 + x_{4}^3 = ( x_{1} + x_{2} + x_{3} + x_{4})^3$$
This in fact simplifies further. Recall that $\mathbb{P}^3$ is the same as $\mathbb{R}^3$ with a plane at infinity, so we ignore the plane at infinity to reduce the surface to a nice real surface in $\mathbb{R}^3$. This is done by removing all points at which the coordinate {4}$ is zero (these points form a plane at infinity) and then scaling the remaining points so that {4} = 1$. Recall from the introduction to projective space (see Algebraic Geometry) that points are equated up to scalar multiples, so we can indeed scale coordinates as we please. Relabelling {1}, x_{2}, x_{3}$ as , y, z$, the surface takes the manageable form $^3 + y^3 + z^3 + 1 = ( x + y + z + 1)^3$$
Symmetry
The surface is invariant under permutations of the coordinates {i}$, and its "symmetry group" {5}$ is the largest symmetry group for any cubic surface, with order 120. Note that these symmetries of the surface cannot necessarily be "seen" just by looking at the model, since they correspond to changes of coordinates in $\mathbb{P}^3$ rather than properties of the real representation of the surface, which is limited to $\mathbb{R}^3$.
Eckardt Points
The Clebsch surface has 10 "Eckardt points" (points at which exactly 3 lines meet). Seven of these are visible on the model: three occur near the bottom, three near the top of the "holes", and one on top in the centre. The other three are beyond the range of our model (recall that the cubic extends to infinity, but it is only possible to make a finite representation of it). In general a cubic does not have any such points, and cubics can have at most ten of them. The Clebsch surface is, remarkably, the only cubic surface with 10 Eckardt points [4].
Passages
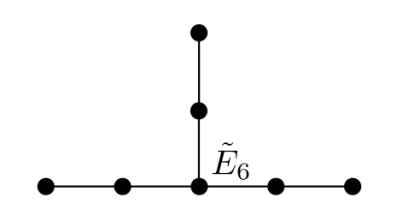
In the model of the Clebsch surface we can see several "passages", to use the archaic nomenclature. Three of these are the holes, one is the thin tube-like piece in the centre, and three are the tube-like pieces directly above the holes. These are in fact much easier to see on our 21st Century Clebsch surface model, below. For each passage there is a homology class on the real surface (we will not discuss the complicated details of what this means here), through which passes a double-six. These passages are "adjacent" if their homology classes intersect, and using this notion of adjacency we can build a graph with 7 vertices. This graph, denoted by {6}$ for the Clebsch surface, is called a "Coxeter–Dynkin diagram", seen below. These graphs have many interesting properties. For instance, a configuration of rational double points may occur if and only if its Coxeter–Dynkin diagram is a subgraph of $\widetilde{E_{6}}$. Coxeter–Dynkin diagrams are explored in detail in the context of cubic surfaces by Gerd Fischer in his excellent account of mathematical models [5]. There are mamy other different properties of the cubic which relate to the 27 lines, some requiring complicated theory, so we will not explore these in detail. See here for more information on this.
Images: E6 Graph (© "Rgugliel" 2014); Modern Clebsch Surface Model
[show-siblings]
References
[1] A. Cayley, On the triple tangent planes of surfaces of the third order, Cambridge and Dublin Math. J., 4 (1849), 118–138.
[2] Clebsch, A. (1871), "Ueber die Anwendung der quadratischen Substitution auf die Gleichungen 5ten Grades und die geometrische Theorie des ebenen Fünfseits", Mathematische Annalen 4 (2): 284–345, doi:10.1007/BF01442599
[3] Schläfli, L. An attempt to determine the twenty-seven lines upon a surface of the third order, and to divide such surfaces into species in reference to the reality of the lines upon the surface, Quart. J. pure appl. math., vol. 2 (1858), 110–120.
[4] Hunt, B. The Geometry of Some Special Arithmetic Quotients. New York: Springer-Verlag, pp. 122-128, 1996.
[5] Gerd Fischer. Mathematical Models, Commentary. Vieweg & Sohn, first edition, 1986.
[6] Artifacts of Research: On Singularities, Addendum: The Clebsch Diagonal Surface Configuration, Jonathan D. Chertok (Universal Joint), 2008
[7] Polo-Blanco, I. (2007). Theory and history of geometric models, section 2, Theorem 2, p31, s.n. https://www.rug.nl/research/portal/files/2803507/thesis.pdf









