Hessian Surfaces

Brief introduction to Hessians

The Hessian matrix was developed in the 19th Century by German mathematician Otto Hesse, after whom it is named. It is an important tool in differential geometry, describing the local curvature of a function. Given a function (x_{1}, \dots , x_{n})$, its "Hessian matrix" is that of all second order partial derivatives (just think of these as regular derivatives, but for functions of more than one variable), arranged as:

$$\left( \begin{matrix} rac{\partial^2 f}{\partial x_{1}^2} & rac{\partial^2 f}{\partial x_{1} \partial x_{2} }& \dots & rac{\partial^2 f}{\partial x_{1} \partial x_{n} }\ rac{\partial^2 f}{\partial x_{2} \partial x_{1} }& rac{\partial^2 f}{\partial x_{2}^2 } & \dots & rac{\partial^2 f}{\partial x_{2} \partial x_{n} } \ dots & \dots & \ddots & dots \ rac{\partial^2 f}{\partial x_{n} \partial x_{1} } & rac{\partial^2 f}{\partial x_{n} \partial x_{2} }& \dots & rac{\partial^2 f}{\partial x_{n}^2} nd{matrix} ight)$$

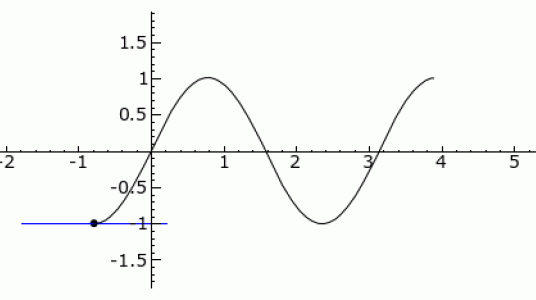
A "point of inflection" on an algebraic surface is defined by how the surface intersects its tangent space. Such a point generalises the more familiar notion of a point of inflection on the graph of a function: a point at which the function changes between convex and concave or vice-versa. Here, the tangent to the curve meets it "with greater intersection multiplicity" than at a smooth point. At such a point on a curve, the curvature vanishes - it is approximately straight if you 'zoom in' sufficiently close. Click the animation below to see inflection points highlighted on a sine curve:

A particularly powerful result is that for a curve defined by (x_{1}, \dots , x_{n}) = 0$, the inflection points are exactly those smooth points at which the determinant (an important polynomial whose variables are the entries of a square matrix) of the Hessian vanishes. Given a cubic surface, its corresponding "Hessian surface" is the surface of points at which the determinant of the Hessian matrix vanishes. Finding the points of intersection of a surface (or variety) with its Hessian hence yields all of its points of inflection.

The Hessian surface is a "covariant" of a surface, meaning that the Hessian surface has the same symmetries as the original surface [2]. The shared symmetry is evident when comparing VII 2 with VII 24a: each has three-fold rotational symmetry and three planes of reflection.

For a cubic surface, the Hessian is always a quartic surface (defined by an order 4 polynomial). This is because the Jacobian is a $4 imes 4$ matrix over projective coordinates. Given a smooth cubic, its Hessian has 10 ordinary double points. For each double point on a singular cubic, the Hessian gets in addition to its 10 double points another "node" (a special type of singularity). For the Hessian of the Cayley cubic (Model VII 2) there are 14 nodes, not all of which are shown on the model.

The "Sylvester pentahedron" is a special collection of 5 planes through a cubic surface, and was an object of interest in Carl Rodenberg's PhD thesis [1]. In 1851, English mathematician J.J. Sylvester conjectured that a degree 3 polynomial in 4 variables can be written as a sum of 5 cubes of degree one polynomials. This was later proven by Clebsch. Each of these 5 polynomials defines a plane, and together they form the "Sylvester Pentahedron" for a cubic surface. These 5 planes are not tritangent to the cubic (intersecting in three lines), but they have the similar property of meeting its Hessian surface in four lines each.

The Models

Model VII 24a is a quartic surface depicting the Hessian for the Cayley cubic (VII 2). It is missing a small piece which should sit in the centre, above the smallest remaining piece.

Model VII 24b is an elegant model with interesting symmetry, depicting the small star-shaped piece in the centre of 24a, for the case where the Sylvester pentahedron consists of a regular tetrahedron and a plane at infinity. Beyond this explanation, the mathematical significance is not particularly simple - see [1] for more details. 

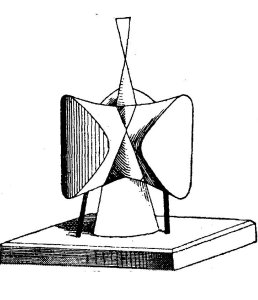
Model VII 25 is the Hessian for VII 5, and we have two identical copies of this model. It is again missing a small piece which should sit in the centre above the smallest remaining piece, as illustrated below (drawing from the Schilling catalogue [3]).

[1] Rodenberg, C. "Zur Classification der Flächen dritter Ordnung." Math. Ann. 14, 46-110, 1878.

[2] B. Hunt, A Gallery of Algebraic Surfaces (2001), http://arpam.free.fr/hunt.pdf

[3] Martin Schilling : Catalog mathematischer Modelle für den höheren mathematischen Unterricht. 7. Aufl. Leipzig, 1911.